虐完了轮胎动力学,如果你觉得自己水平可以了,那就来挑战车辆动力学吧!
关于本文重点所谈及的,对于由预先给定的转向输入作用下所产生的车辆运动响应,已经有了大量的研究成果。这些研究为车辆动力学奠定了坚实的基础——其经典著作包括有:
-
美国的《Race Car Vehicle Dynamics》(William & Douglas)
-
德国的《Dynamik der Kraftfahrzeuge》(Manfred & Henning)
-
日本的《自動車の運動と制御》(安部正人)
其中,RCVD这部硬通货,是几乎所有赛车理论书籍的“源头活水”。
对于工程师而言,设计出优良操控的汽车,需要探求各种理论的边界条件,是一项游走在极限上的艺术。即便是专业赛车手,也需要不断在车辆的极限上”修正”和”挑战”自己的操作,从而达到人车合一的程度。
先理解那些伟大的思想,这比批判它们,往往要困难得多。然而,搞研究毕竟不是搞科普,三部经典不必全部读完。科学训练最重要的不是公式,而是培养对科学工作的品味和直觉。真正重要的——是认知。
当我们有大把的时间,散着步去计算宇宙的孤独和寂寞,那么就来钻研汽车动力学吧,前人的经验,加上独立的探索和思考,不光能够打开心智,稍加练习,你甚至还能习得一手收放自如的王者飙车风范。
跟着感觉,选出一本,深入学习并精通掌握,去搞清楚并解决问题。
不把信息当作知识,不把收藏当作学习,不把阅读当作思考,不把存储当作掌握。
不提炼总结,不应用学习,不深入思考,不实践反馈,就不是自己的能力。
只需要搞定一本书,就是一个好的不能再好的开始!如果你的选择也是——我最偏爱的《自動車の運動と制御》这部硬通货,就让我们一同开始吧!
壹
车辆运动方程与耦合直觉
为车辆运动建立方程,大体有两种视角:
-
固定于车辆坐标系下的运动方程
-
地面固定坐标系下的运动方程
对于一个特定的刚体运动来说,选择合适的坐标系是最重要的——因为,通过巧妙地定义坐标系,可以简化对该刚体运动的描述。
简化问题需要一些原则,这个前提就是不将问题的本质丢失。这可以包括(这些内容将在今后做独立研究):
-
忽略车辆的瞬态现象,比如突然的加速和减速
-
忽略大幅度急转转向盘的情况
-
忽略车辆的垂向高度和侧倾的情况
如此一来,这个模型可以被看作是投影在地面上的刚体,我们就可以将重点放在车辆的侧向运动和横摆运动的研究上。
平面内运动的车辆,相比固定于地面的坐标系而言,车辆的纵向和侧向是持续变化的。因此从车的视角观察,不管车辆朝什么方向运动,其运动约束基本是不变的。因此用固定于车辆坐标系下描述运动更加简便。
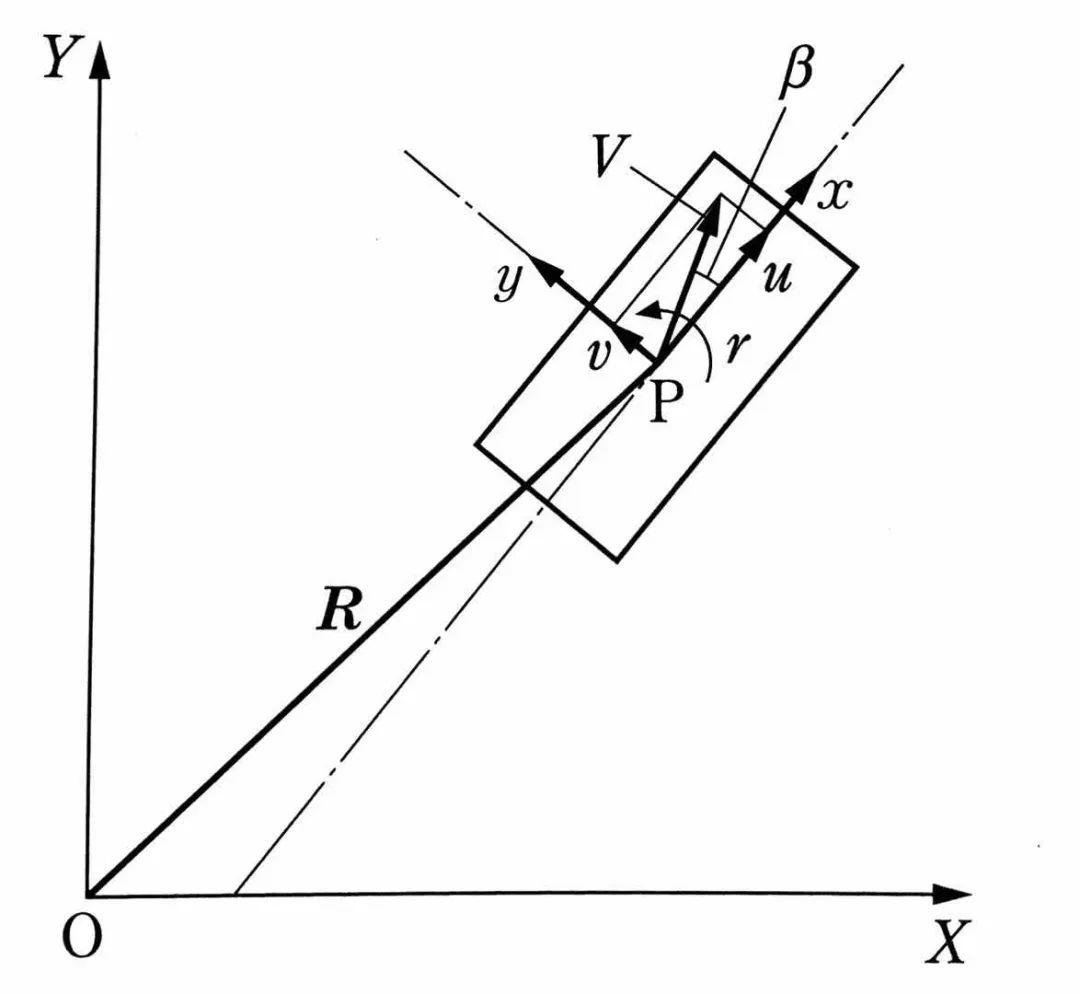
如上图所建立的坐标系所示,P点的加速度矢量R”可以表达为:
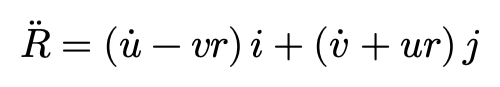
车辆的行驶方向和纵向夹角β可以表达为arctan(v/u),我们称其为车辆的质心侧偏角。对于普通轿车来说,因为u>>v,因此可以认为|β|很小,而且,如果车辆行驶速度是恒定的,则V=√(u^2+v^2)也是一个常数。
于是得到以下表达:
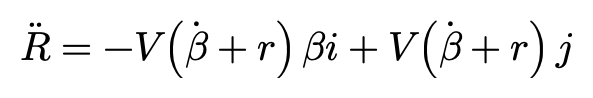
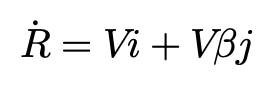
可以发现,以上两个矢量R”和R’的点积等于零,也就是说,R”正交于R’(即P点的行驶方向),当β很小的时候,P点有一个垂直于车辆行驶方向(沿y方向)的大小为V(β’+r)的侧向加速度,其中r为绕质心的角速度。
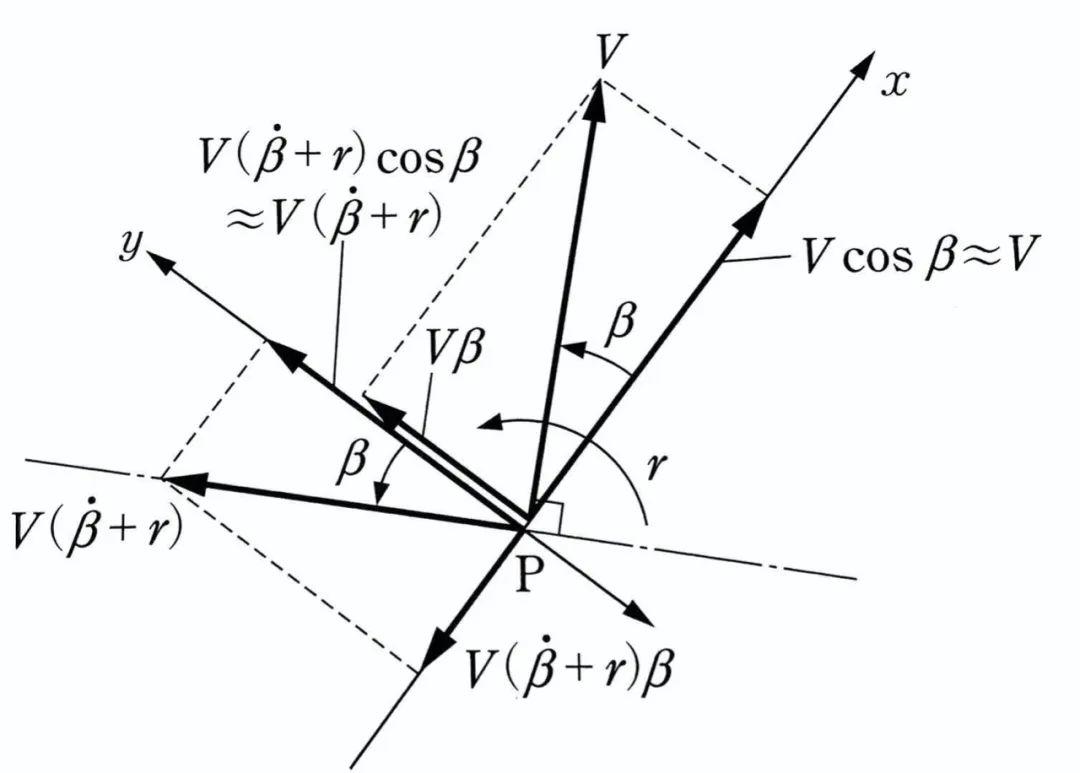
由于车辆的侧向运动和横摆运动会在轮胎上产生侧偏角,对应轮胎的侧偏角轮胎会产生一个侧偏力,而由车辆运动产生的侧偏力又回反过来成为控制车辆运动的力。侧向运动可以描述为:
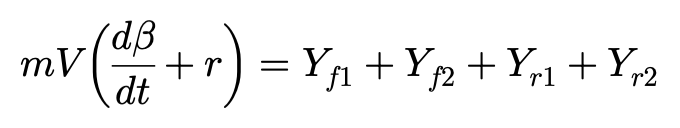
Y代表四条轮胎的侧偏力,m为车辆的惯性质量。
同时,侧偏力产生绕质心的横摆力矩,可以表达为:
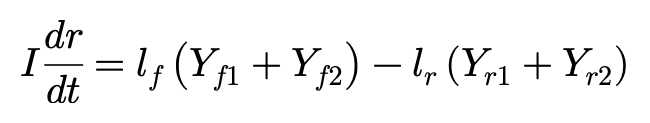
I为车辆的横摆转动惯量,lf和lr分别车辆质心至前后轴的距离。
以上两个方程,就是描述车身无侧倾时,车辆以恒定速度做平面运动的基本模型。
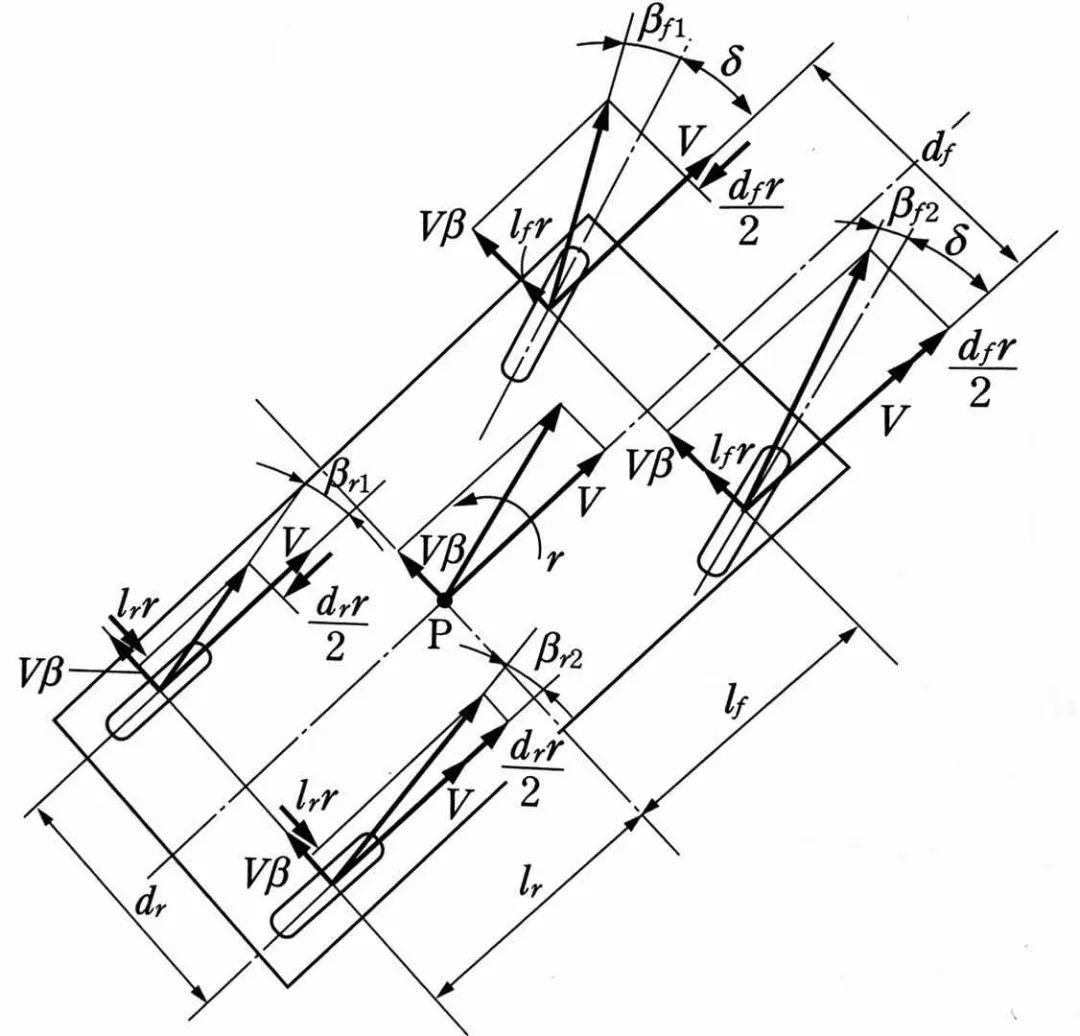
如果更细致地分解四个轮胎的侧偏角和侧偏力,并考虑前轮相对于x方向的夹角——即转向角δ,可以给出以下方程:
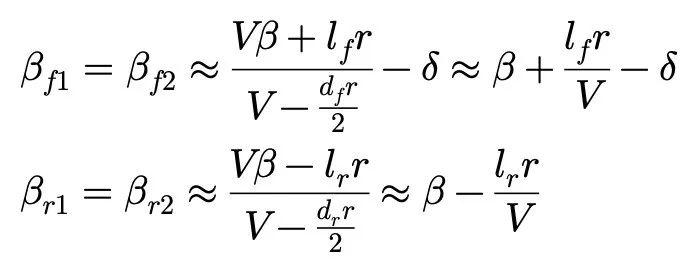
由于Yf1=Yf2,Yr1=Yr2,因此它们也都简化为Yf和Yr表达。于是:
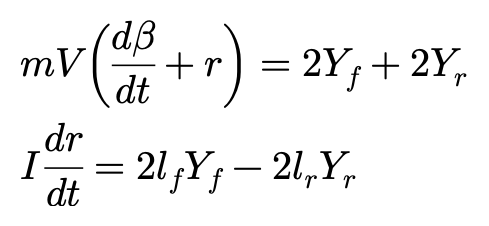
带入侧偏刚度:
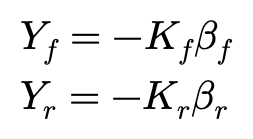
综合以上,得到:
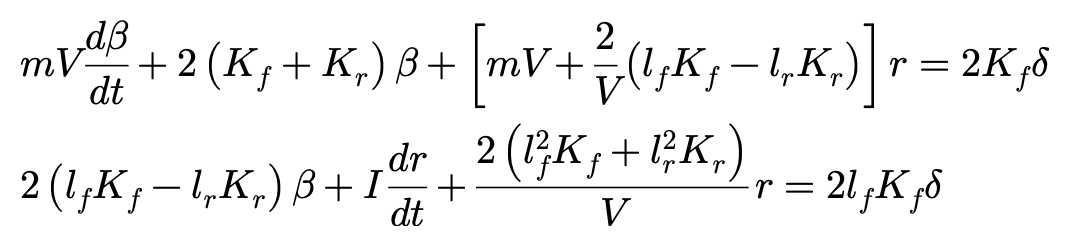
这就是描述车辆平面运动的基本运动方程。
它是关于β和r的一阶连立微分方程。这种形式的方程并非汽车独有,实际上,转向时,对于独立运动的船舶,也可以用这个数学形式来表达。依靠升力的飞机运动,尤其是纵向运动,也能够看到类似的动力学方程。
相对于右面给定的转向角δ,方程左边描述了车辆的相应运动特性。从这个方程还可以发现,车辆的运动并不受其相对于地面固定坐标系位置或航向的影响。
此外,还有一个更重要的发现:系数lfKf-lrKr对车辆运动有很大的影响。如果这个值为0,则表示车辆的侧向运动与横摆运动完全不耦合——β和r没有相关性。
对以上两式进行拉普拉斯变换,用s来表达拉普拉斯算子,可以得到车辆运动的特征方程为:
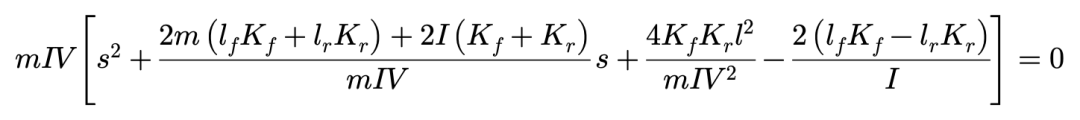
接下来,我们变换视角,考察以固定地面坐标系表达的车辆运动。在某些情况下,比如恒定速度直线路面行驶条件下,这一视角表达的车辆方程会更加简单。
在这一视角下,设地面坐标系X轴与车辆纵向的夹角(即车辆的横摆角)为θ,X轴与车辆航向的夹角为γ。
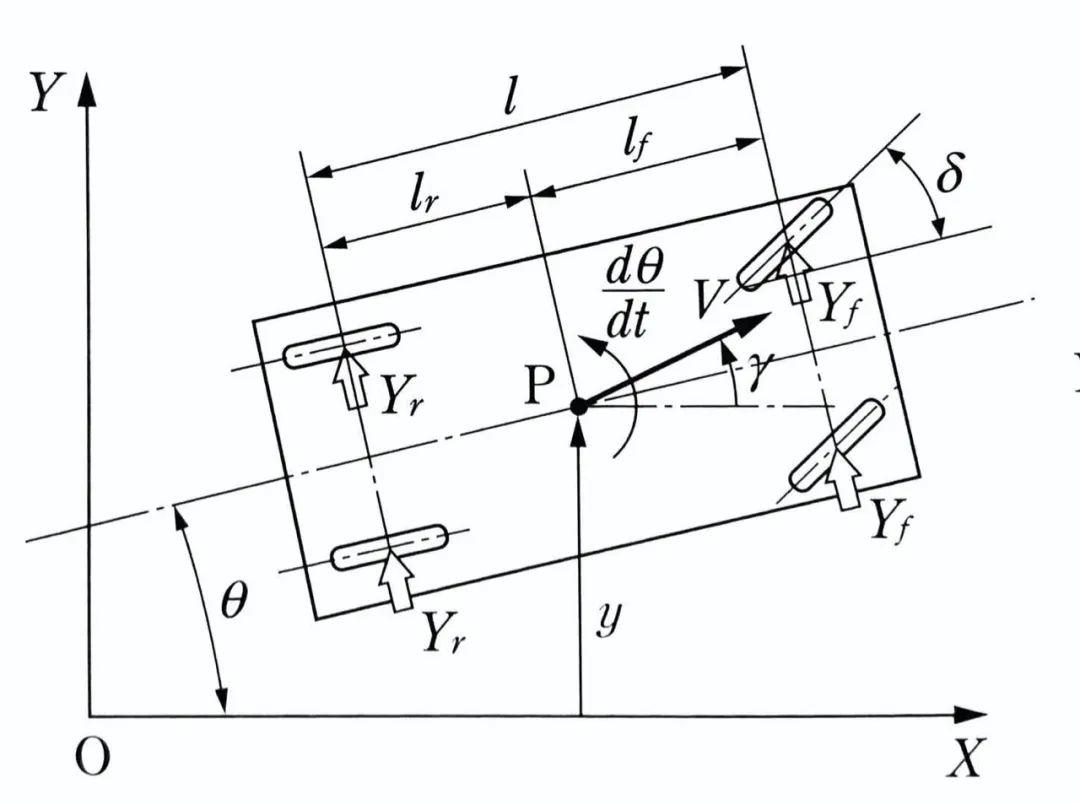
这一设定下,有:
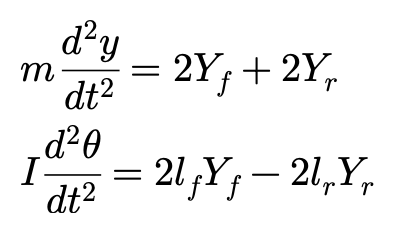
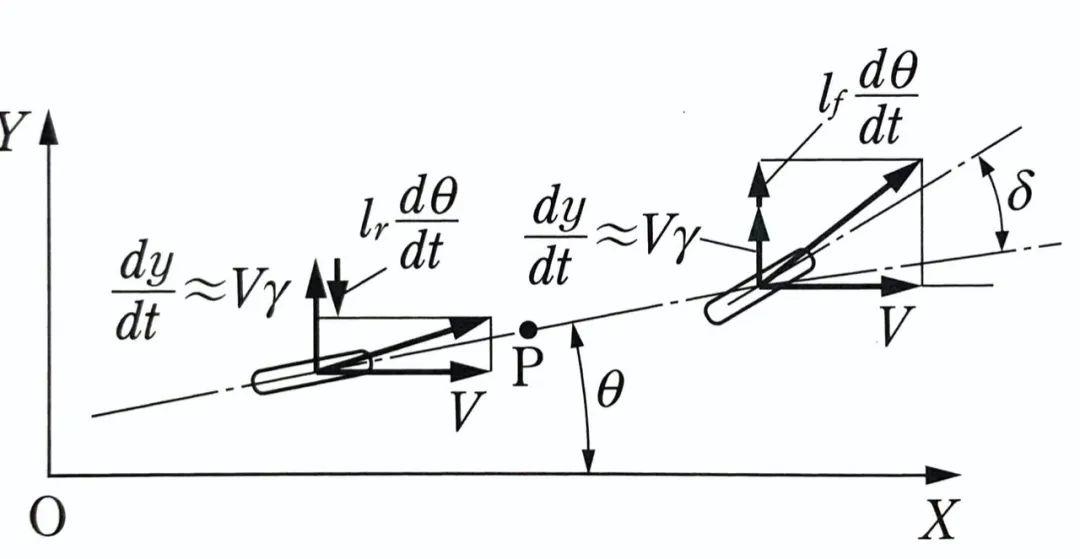
对前后轮而言,行进方向分别存在一个相对X轴的夹角,分别为:
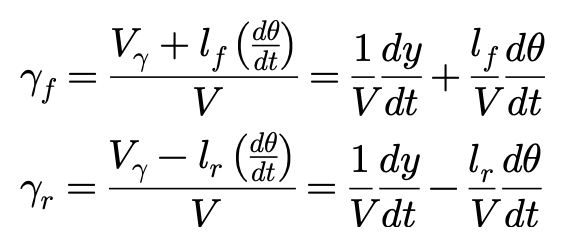
前后轮的侧偏角可以表达为:
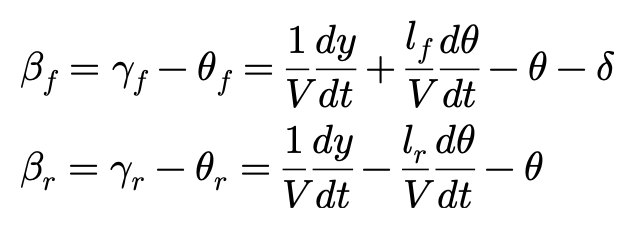
综合以上,带入刚度,得到:
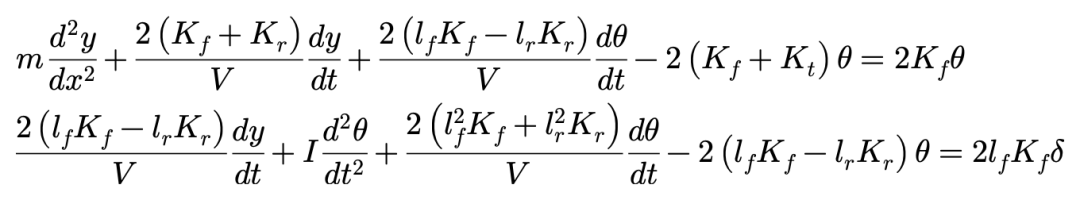
这就是地面固定坐标系下车辆的运动方程。
同样可以发现,对于方程右侧给定的转向角δ,方程左侧的系数lfKf-lrKr影响着侧向位移y和横摆角θ的耦合状态。可见,这一系数与坐标系无关,是车辆运动方程当中一个重要的特征,关于这个系数的理解,我们将随后展开讨论。
对运动方程做拉普拉斯变换,得到:
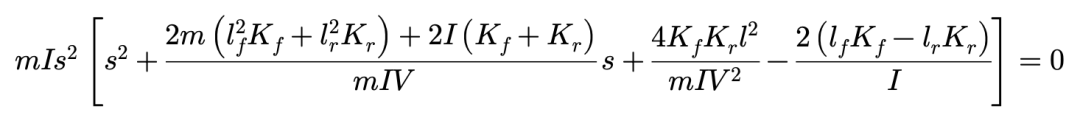
如果省略掉中括号外的s^2项,这与整车坐标系下的特征方程完全一致。这意味着:不论选取的坐标系固定于车辆还是固定于路面,车辆运动描述的本质是完全一样的。
这个s^2项意味着,无论在至路面的何处,车辆都能通过转向而自由行驶——变换车道或者躲避障碍。同时,如果不对车辆施加适当的转向操作,由某些外部干扰引起的路径侧向偏离|y|,将不断增大,从而导致车辆偏离目标轨迹。
贰
稳态转向与运动特征直觉
简化的车辆模型有很多,包括但不限于:
-
恒定速度模型(CV,Constant Velocity)
-
恒定转向速率和速度模型(CTRV,Constant Turn Rate and Velocity Magnitude)
-
恒定转向速率和加速模型(CTRA,Constant Turn Rate and Acceleration)
-
恒定转角和速度模型(CSAV,Constant Steering Angle and Velocity)
-
恒定曲率和加速模型(CCA,Constant Curvature and Acceleration)
不同的模型都有着不同的假设条件,在这里,我们将重点研究稳态转向的内容——即以固定转向角及恒定的速度行驶的车辆做等曲率半径稳定圆周运动的CSAV情形。
一般来说,为了从理论上理解一个力学系统的特性,可以通过考虑在适当初始条件下,对其运动方程的求解来实现。
但往往运动方程太复杂,无法获得解析解。即便通过计算机可以对运动方程进行数值求解,但我们却也因此而丧失了对车辆运动的直觉性理解——这是得不偿失的。
于是我们诉诸于两种方法,绕过直接求解,通过运动方程获取运动特征的直觉:
-
分析力学系统的稳态条件,了解静态特征
-
考察该力学系统的特征方程的特征根,以及对周期性外界干扰的响应,研究动力学特征
这一节,我们先来通过稳态条件看静态特征。
在CSAV模型的限定下,车辆做稳态转向运动,这意味着,车辆质心侧偏角β和横摆角速度r是恒定不变的——即dβ/dt=0;dr/dt=0。
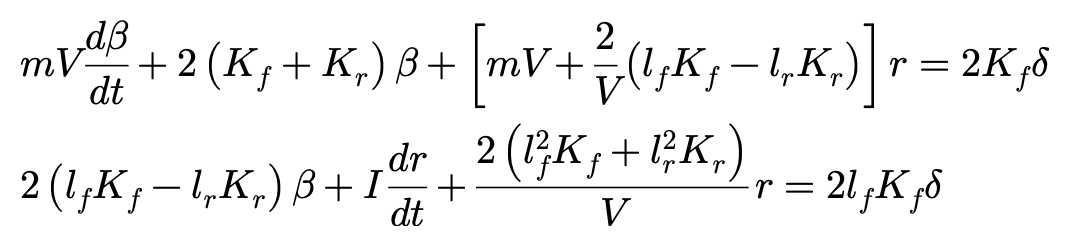
因此,以上整车坐标系下的运动方程可以简化为:
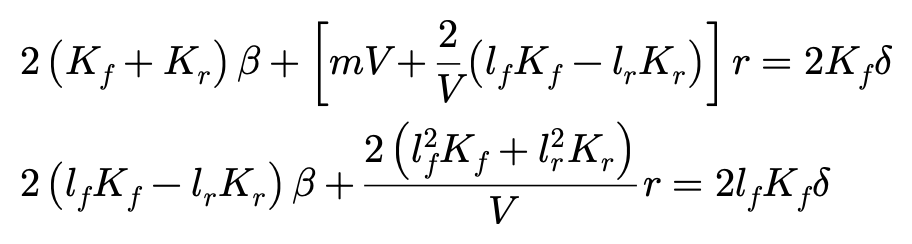
求解β和r得到:
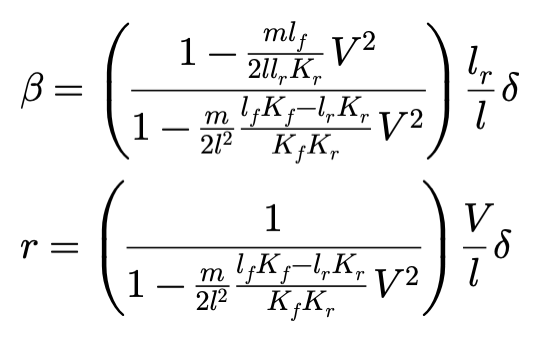
已知车速V,则CSAV条件下的稳态转向半径ρ为:
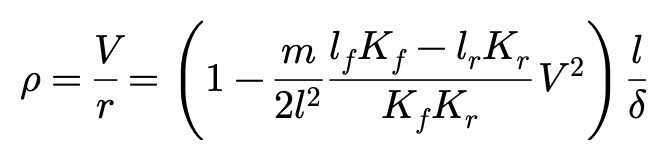
解析之后,我们再从几何学的角度来理解CSAV模型。
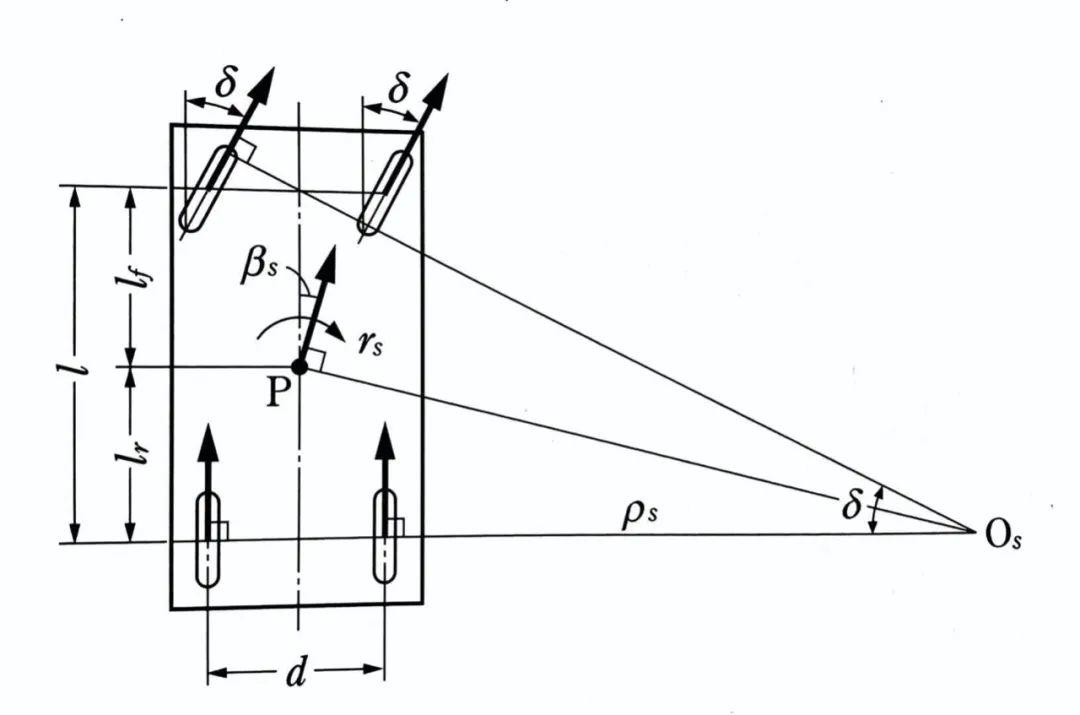
在极低速条件下,即V趋近于零时,β,r,ρ的表达可以简化为:
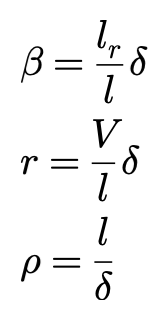
由于车辆以极低的速度蠕行,因此没有侧向力的作用,无侧偏角产生,无离心力产生,车辆绕Os点做圆周运动。
在这种情况下,左右前轮真正的转向角并非δ,而是左边要比δ稍小,右边的转向角比δ稍大。
以上的关于δ的几何学关系就是我们耳熟能详的阿克曼转向几何学。而δ=l/ρ就被称为阿克曼转向角。
当汽车以高速作圆周运动时,以上关系将不再成立,车辆将明显受到离心力的影响,为了克服离心力,就要求前后轮的侧偏力来平衡,因此,前后轮将产生侧偏角。
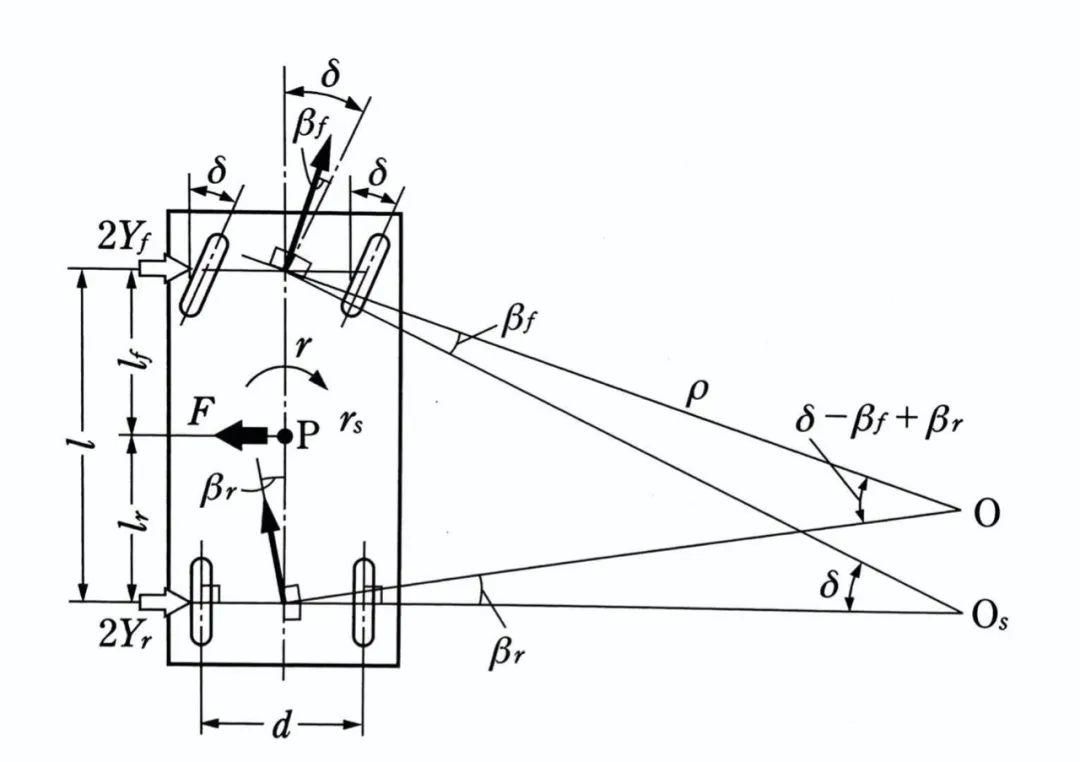
如图所示,车辆做圆周运动的中心分别垂直于前后轮行进方向两条直线的焦点O,几何关系为:
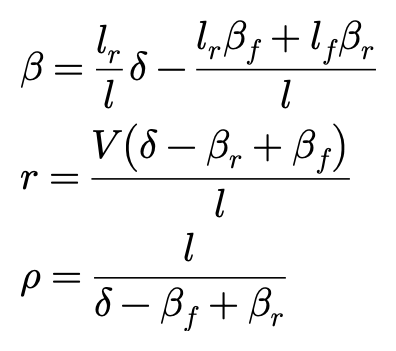
βf和βr作为前后轮侧偏角,可以由作用于车辆质心的离心力求出,离心力取决于车速V的大小。于是,β,r,ρ都将随着车速V的变化而改变。
稳态转向条件变化的原因,是由于离心力随车速V的变化而改变,从而引起前后车轮侧偏角β改变,反过来又由此引起圆周运动几何学及稳态转向条件(r和ρ)发生变化。
值得一提的是,β,r,ρ的表达都是来自几何学分析,这些方程不受侧向力和侧偏角(βf和βr)关系的影响,也不受到任何前后车轮侧向力的影响。只要|δ|<<1,ρ>>l,这些方程在任何情况下都有效。
而前面所得到的解析表达则严格受到前提条件的制约:作用于前后轮的侧向力正比于侧偏角。
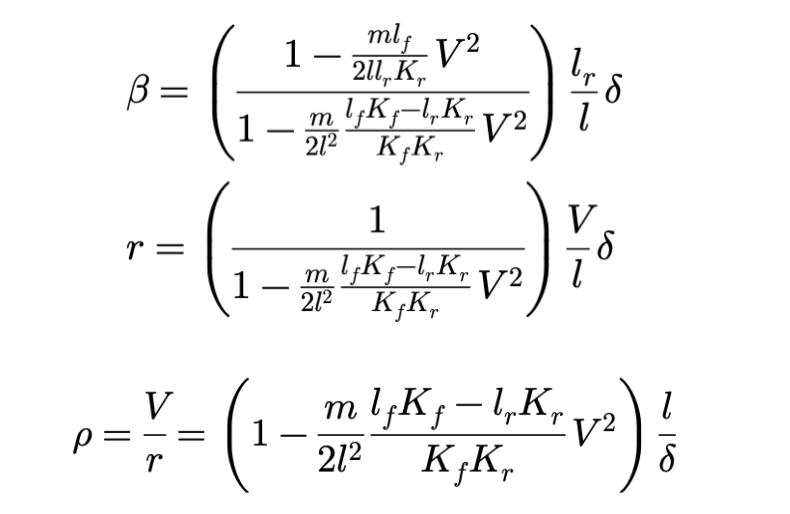
同样可以证明的是,根据稳态转向几何学描述可以推导出上面的方程。
开始计算,如果让前后轮侧偏力抵消离心力,则有:
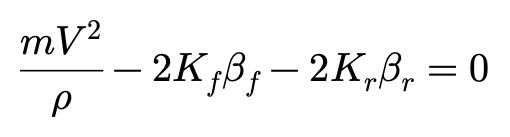
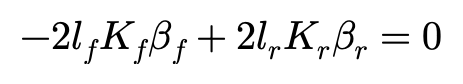
求解方程得到:
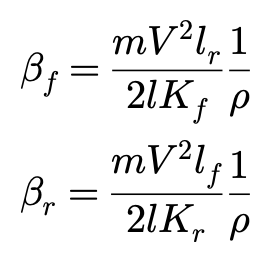
将此解带入几何表达:
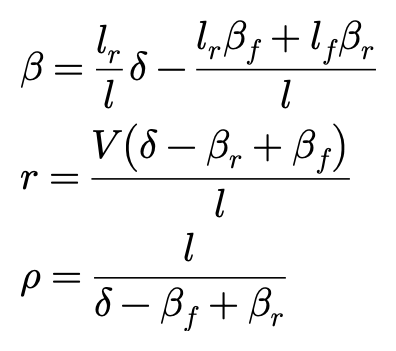
得到的不是别的,正是解析表达:
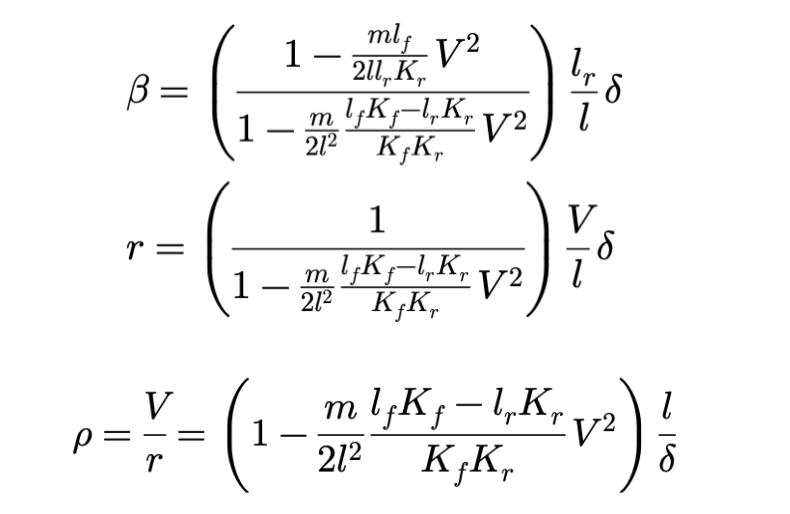
叁
转向特性的运动直觉
从CSAV条件下的稳态转向半径ρ出发:
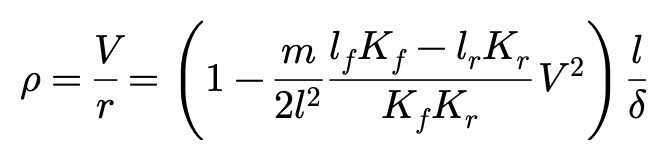
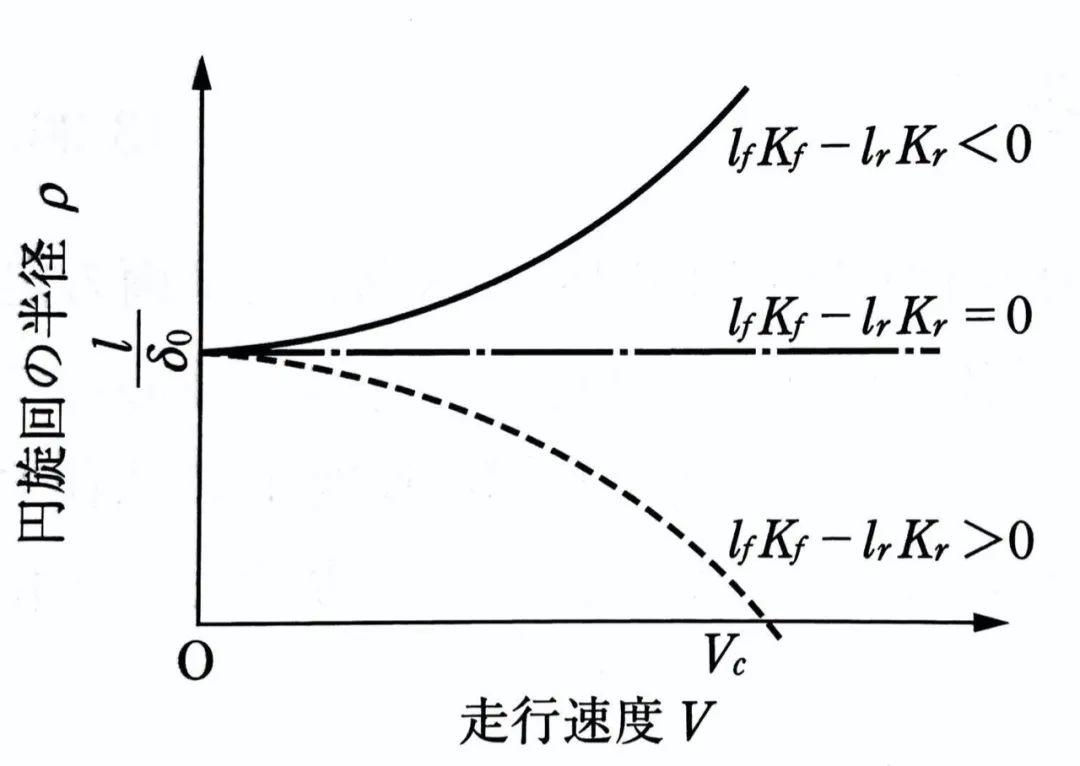
这个方程可以推倒出固定转向角情况下,系数lfKf-lrKr对于车速和转向半径之间关系的影响:
-
lfKf-lrKr <0时,车辆转向半径ρ随着车速V的增加而增大
-
lfKf-lrKr =0时,车辆转向半径ρ与车速V无关
-
lfKf-lrKr >0时,车辆转向半径ρ随车速V的增加而降低,当车速进一步增加到V=Vc时,ρ=0,此时意味着车辆将无法转向。
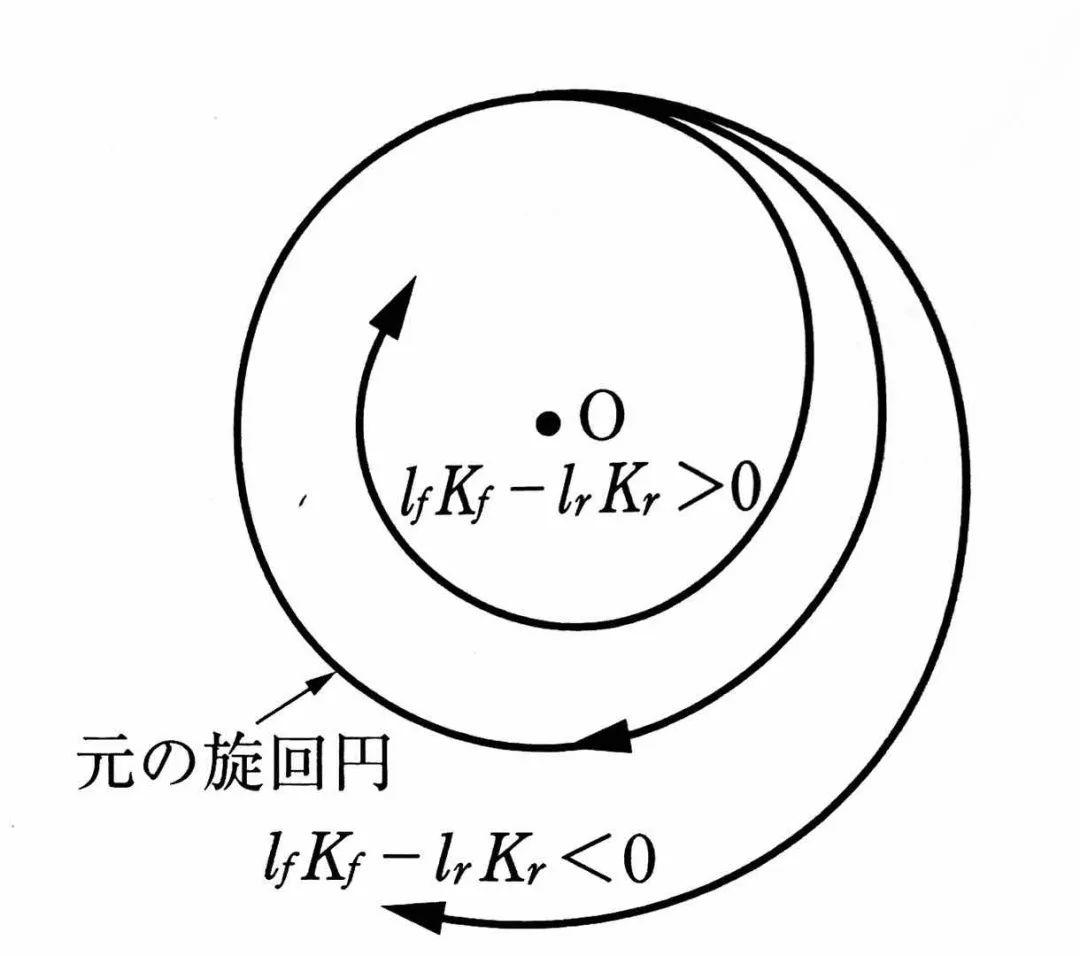
关于上面lfKf-lrKr 系数不同的引起的三种不同车辆轨迹,还有着一类众所周知的称谓:
当lfKf-lrKr <0时,如果保持转向角不变而增加车速,要想维持原来的圆周路径半径,转向角就显得不足。这样一种相对车速的增加转向角呈现不足的特性,就被称作不足转向特性(US)
类似地,lfKf-lrKr >0时,是过度转向特性OS,lfKf-lrKr =0时,是中性转向特性(NS)。
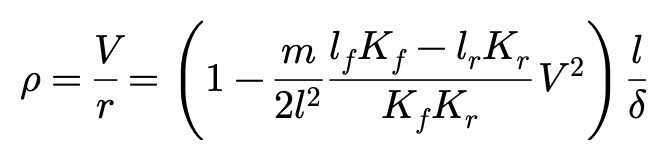
颠倒δ和ρ,把以上方程转化为:
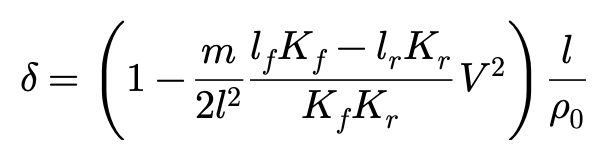
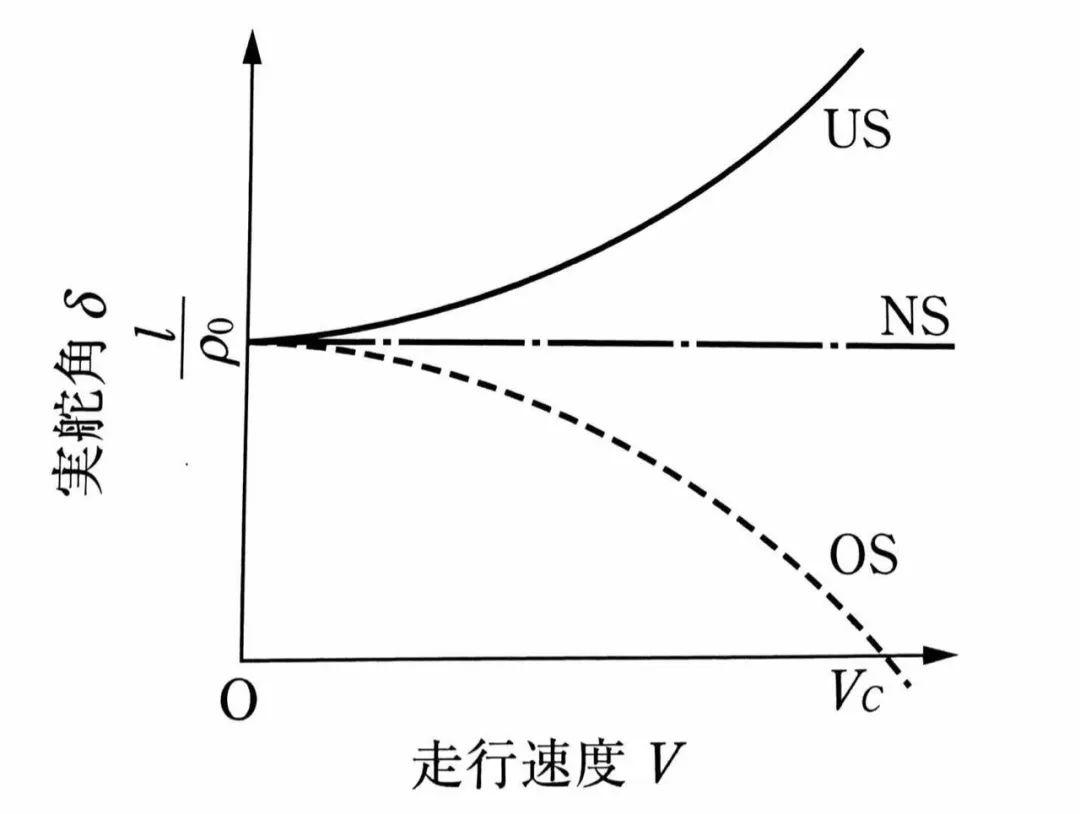
这张图告诉我们,当侧偏力正比于侧偏角,并且侧偏力是仅有的左右在前后轮上的力时,车辆的圆周运动很大程度上,受到lfKf-lrKr 的影响。
要使车辆维持作固定半径的圆周运动:
-
lfKf-lrKr <0时,必须随车速增加而增大转向角
-
lfKf-lrKr =0时,转向角与车速无关
-
lfKf-lrKr >0时,必须随车速增加而减少转向角
同样的公式,转换后,再来看横摆角速度r与车辆转向特性的关系:
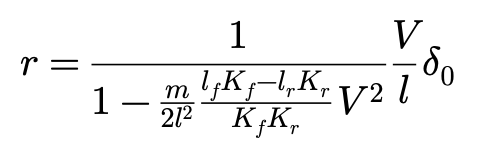
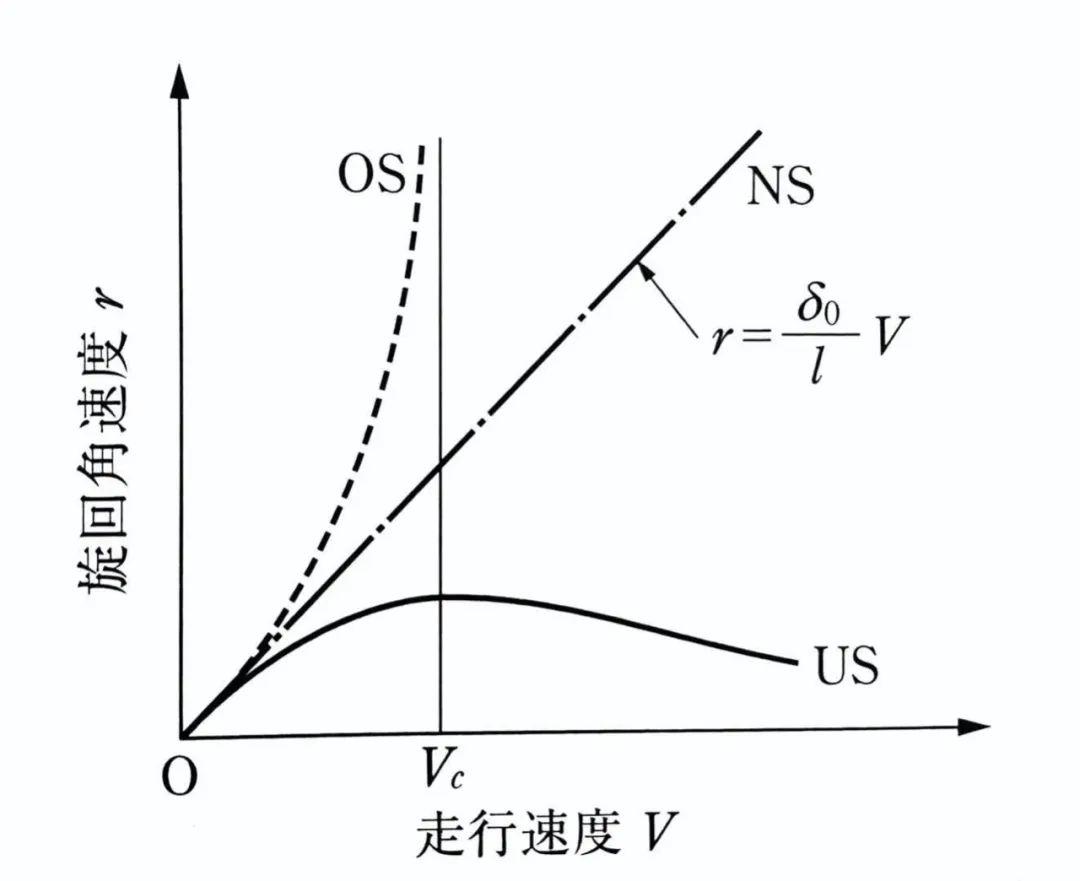
这张图告诉我们:
-
具有NS特性的车辆,横摆角速度r随车速V呈线性增长
-
具有US特性的车辆,横摆角速度r随车速V增加而增加,当车速进一步增加到某一个值时,横摆角速度将趋于饱和不再增大
-
具有OS特性的车辆,横摆角速度r随车速V的增加迅速增大,在某一车速Vc将趋于无穷大
最后,则考察质心侧偏角β与车辆转向特性的关系:
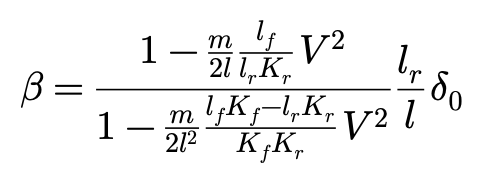
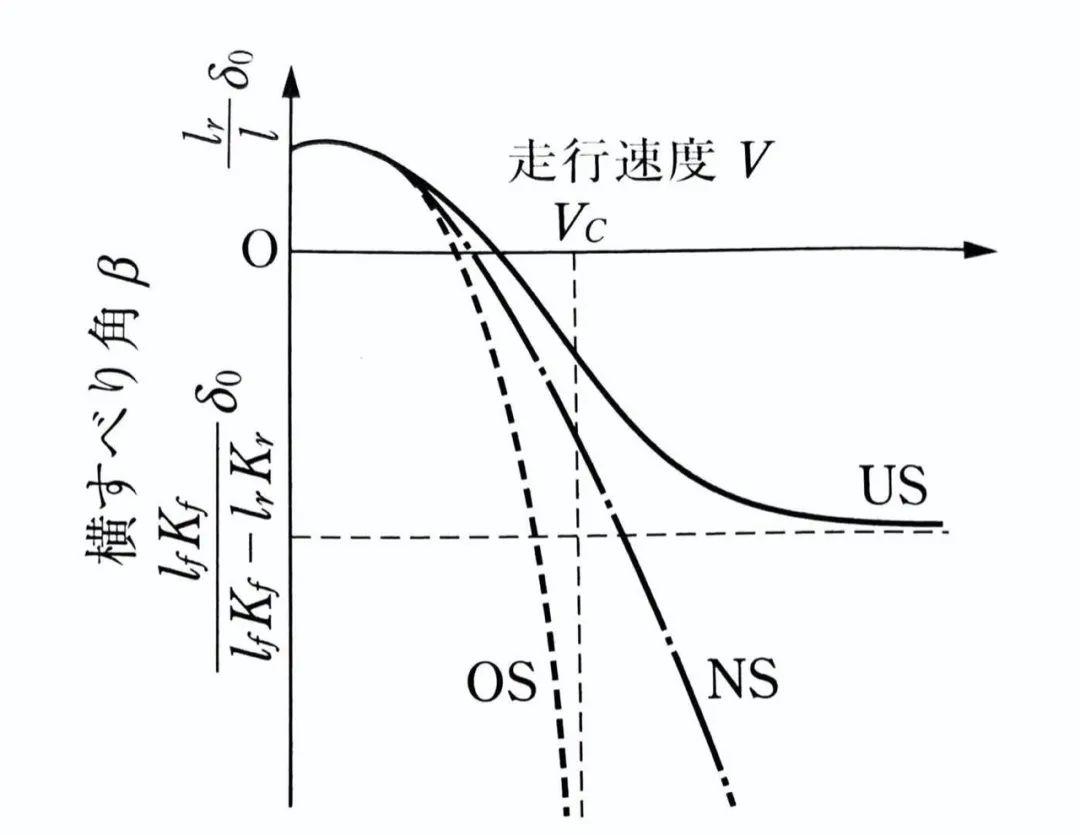
图上告诉我们,不论车辆的转向特性如何,质心侧偏角β都随车速的增加而减小。
超过某一车速后,β值变为负值,其绝对值会增大。
-
如果车辆呈OS特性,则β在V=Vc处变为无穷负值。
-
如果车辆呈US特性,则β会在某个较高的车速达到饱和
-
如果车辆呈NS特性,则β为以下表达式:
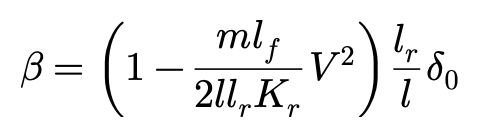
正如前文提到的:车辆质心的侧偏角β之所以随车速变化而与车辆的转向特性无关,原因在于,车辆需要侧向力来平衡离心力。
β角代表的是车辆纵向与车辆质心行驶方向之间的夹角,随着车速的增加,β值将由正值(左图,低速)变为负值(右图,高速),这意味着,当车速增加时,车头会逐渐指向圆周运动轨迹的内侧。
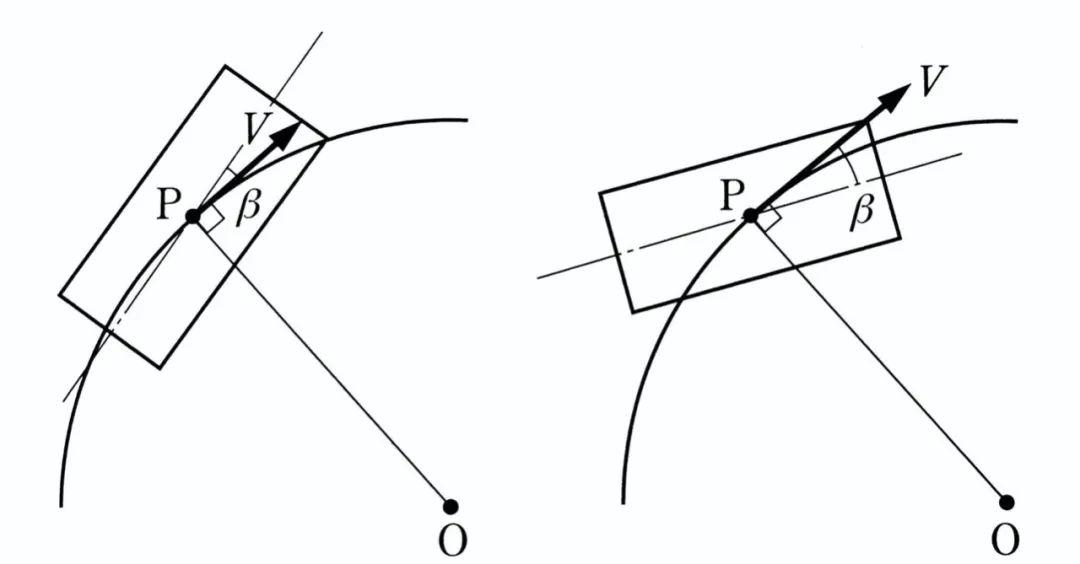
越是具有OS特性的车辆,这种趋势会愈加明显。
再次回到第二节当中CSAV条件下的β表达:

将其与CSAV条件下以下方程联立:
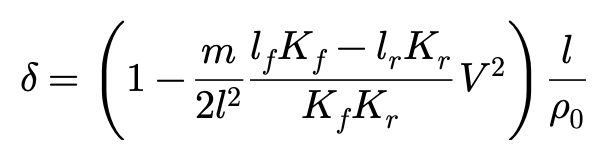
消去δ,得到:
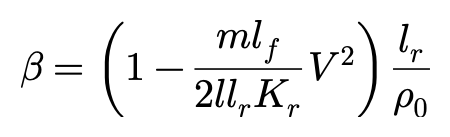
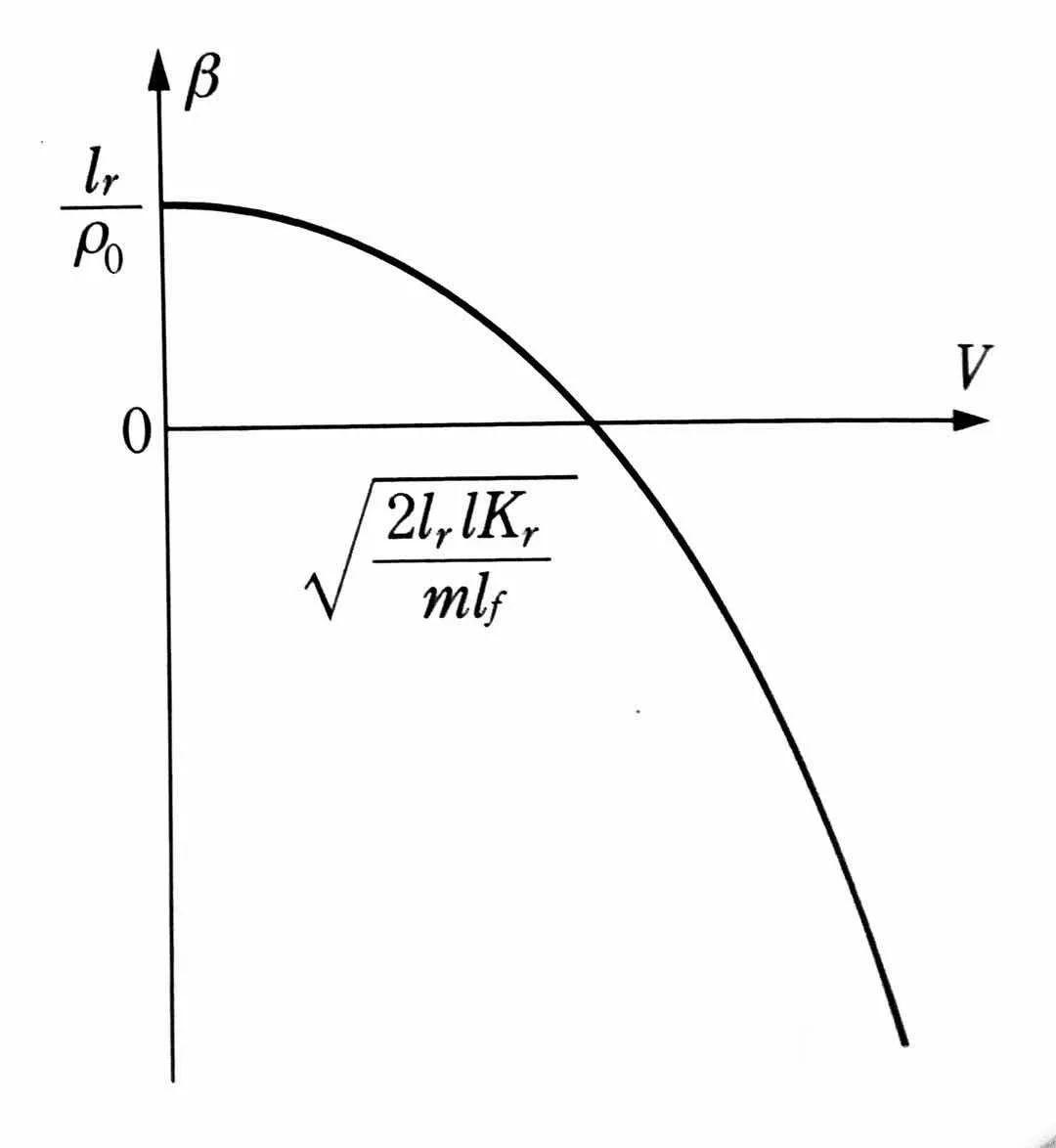
质心侧偏角β相对车速V的变化
从这个方程可以看出,当车辆作固定半径ρ0的稳态转动时,质心侧偏角β随车速变化的规律。有意思的是,相对不同的车辆转向特性,不论是US,US还是OS,侧偏角β随车速变化的情况并无本质区别,原因就在公式本身:侧偏角β的大小只依赖于后轴的侧偏刚度Kr。
肆
稳定临界车速和稳定性因子
当车辆呈OS特性时,相对于恒定转向角,当车辆行驶速度V=Vc时,其圆周转向半径ρ变为0,这时,横摆角速度r和侧偏角β为无穷大。
当车速达到Vc时,β,r,ρ都将不具备物理意义。

Vc可以通过以下方程解出:
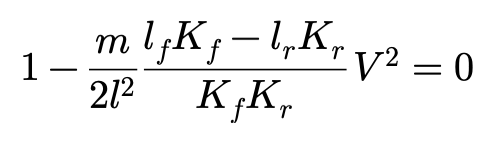
如果lfKf-lrKr>0,则车辆具有OS特性,方程有一个实数解:
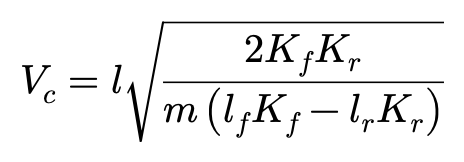
当车速超过Vc时,车辆的圆周运动将不再可能进行下去了。
从公式中还能发现:
-
随着lfKf-lrKr变小,临界车速Vc将增大
-
车辆的惯性质量m越小,临界车速Vc越大
-
前后轮胎侧偏刚度Kf,Kr越大,临界车速Vc越大
-
轴距l越大,临界车速Vc越大
从上式可知,虽然lfKf-lrKr的正负决定着车速对稳态转向特性的影响,但如果车辆的质量m增大,轴距l减小,轮胎的侧偏刚度Kf和Kr减小,同样也会增加车速的影响程度。
需要强调的一点:当汽车呈OS特性,并车速超过Vc时,车辆运动的不稳定性是在前轮转向角恒定的前提下推导出来的,这并不意味着车速在超过Vc后就无法驾驶——此时的车辆是否可驾驭还取决于驾驶者的操纵能力。
基于以上理由,汽车设计者通常倾向于避免设计出呈OS特性的车辆。
在这里我们给出一个新的定义:稳定性因子A
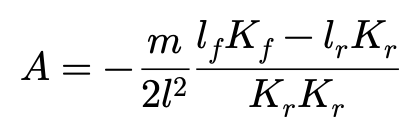
这样,如果A<0,Vc可以表达为:
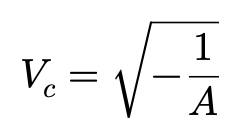
采用新定义,车辆稳态转向运动当中的β,r,ρ可以表达为:
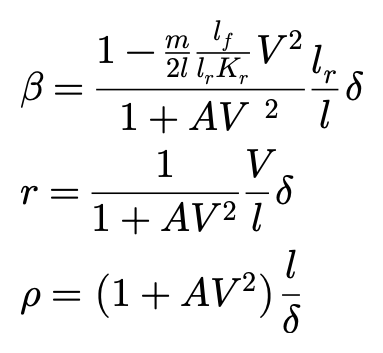
稳定性因子A的符号决定着车辆的转向特性(也被称作US/OS梯度),它是相对于车速的一个表示稳态转向变化程度的重要指标。尤其是当A值固定时,稳态转向响应与V^2成正比。
下面,我们将更加深入地探讨lfKf-lrKr这个数值的物理意义。
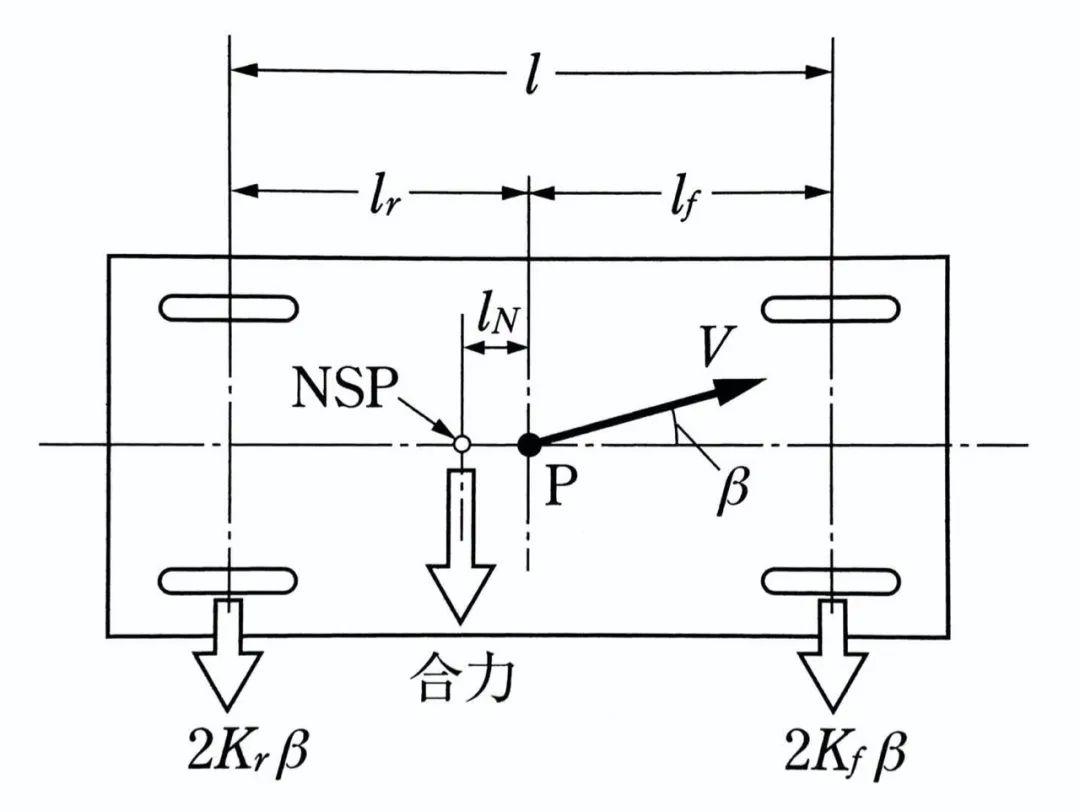
当车辆在δ=0的情况下,由于某种原因产生了质心侧偏角β,并让前后轮同样产生了β侧偏角,于是轮胎出现侧偏力,侧偏力产生绕车辆质心的横摆力矩,可以表达为:
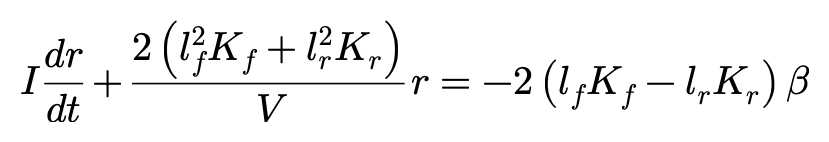
从公式得知,若β为正:
-
lfKf-lrKr为正,合力作用点位于车辆质心前方,一个绕车辆质心的力拒产生负的横摆角速度,即r减小。
-
lfKf-lrKr为零,合力作用点位于质心,无力拒作用。
-
lfKf-lrKr为负,合力作用点位于车辆质心的后方,会有一个绕车辆质心的力拒产生正的横摆角速度,即r增大。
如果将合力作用点称为中性转向点,即NSP,并设NSP与车辆质心的距离为lN,则有:
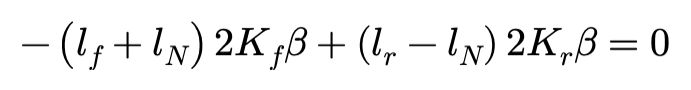
求得:
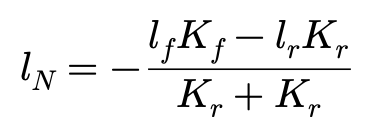
用lN除以轴距l,我们授权这个无量纲的单位一个新的名称:静态裕度(Static Margin,SM),可以写做:
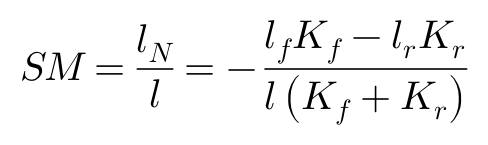
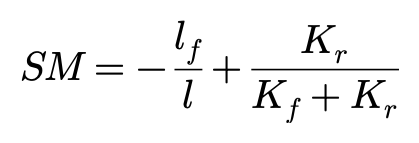
这样,决定车辆静态特性的系数lfKf-lrKr可以采用静态裕度来表达:
-
当SM>0,则为US
-
当SM=0,则为NS
-
当SM<0,则为OS
此外,临界车速Vc(静态不稳定条件)和稳定性因子A也可以用静态裕度SM来表达:
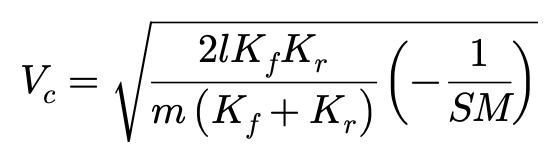
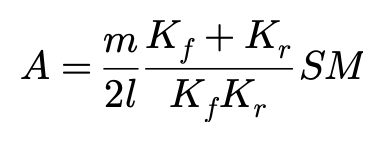
在公式之外,我们还希望针对转型特性进行几何表达。因为以上公式的推导都有一个前提条件:轮胎侧偏力正比于侧偏角。我国同第二小节一样,能够利用几何条件研究车辆的转向特性,是否可以规避这个前提条件,让结论更具普世性呢?
答案是肯定的。
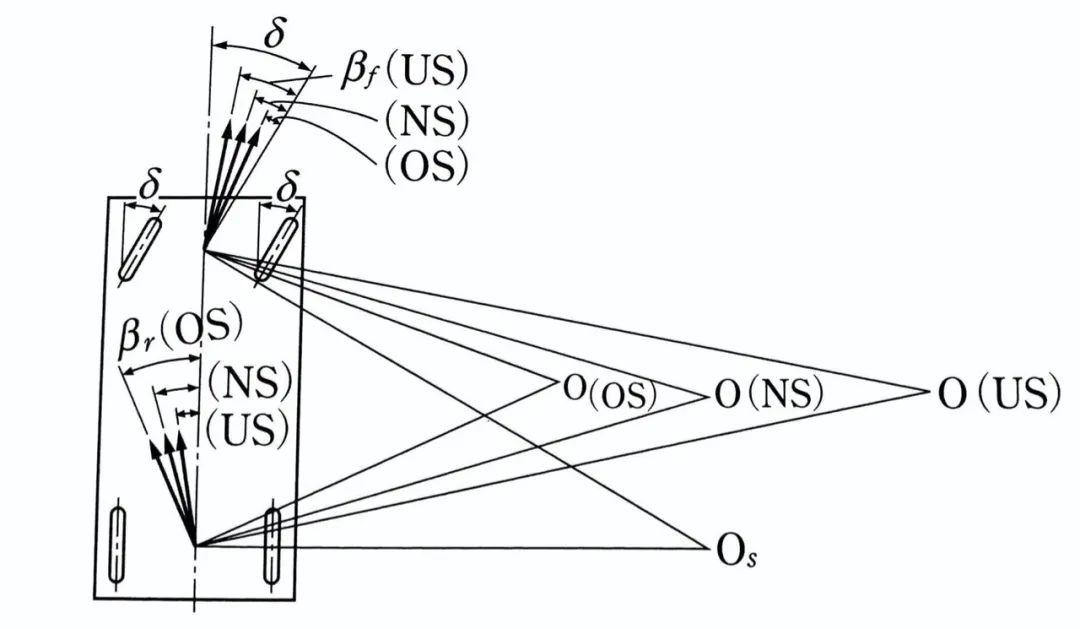
从上图我们可以列出:
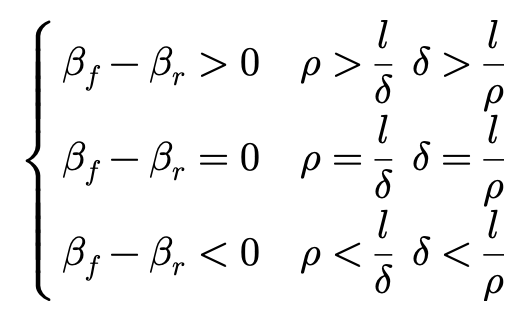
三行分别对应于US,NS和OS。
由于该定义从几何直觉而来,定义不受是否作用有除轮胎侧偏力以外侧向力的影响,与侧偏力是否与侧偏角成正比也无关。
此外,无论车辆具有怎样的转向特性,随着车辆行驶速度的增加,βf和βr均会增大——这印证了前文的结论。在几何上来看,车辆圆周运动的回转中心向车辆前方移动。所以,随着车速的增加,车辆会向圆周的轨迹内侧偏移。
从图上,可以得到几何表达:
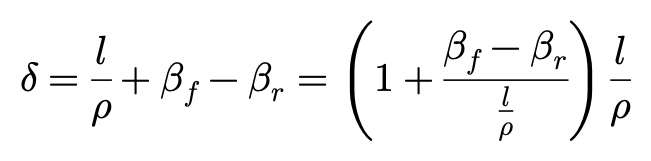
当前后轮产生的侧向力仅为与侧偏角成正比的侧偏力时,有:
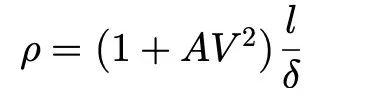
连立以上两个方程,从几何上,稳定性因子可以表达为:
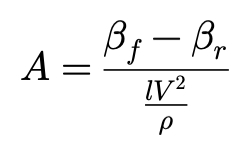
可见,由于V^2/ρ表达的是稳态转向时的侧向加速度,于是稳定性因子所表达的是:转向时单位侧向加速度所对应的前后轮侧偏角之差。
伍
稳态转向与侧向加速度
正因为稳定性因子与侧向加速度有着奇妙的关联,因此,我们想了解,稳态转向与侧向加速度之间的关联。
稳态转向时,侧向加速度可以表达为:
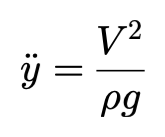
上式必须与作用与前后车轮的侧向力平衡,同时绕车辆质心的力矩为零:
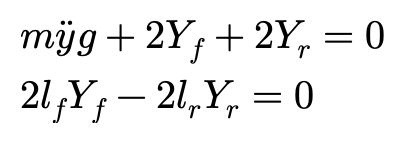
与此同时,假设轮胎侧向力与侧偏角之间为线性关系,得到:
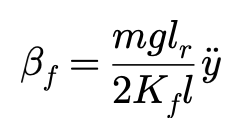
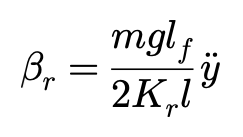
这个表达与第二节结尾的表达有异曲同工之妙。
于是,要想使车辆以恒定转向半径做运动,则其侧向加速度y”与所需的转向角δ之间的关系为:
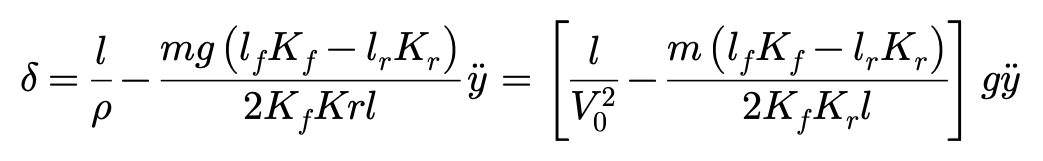
y”的系数可以表达为U,被称作不足/过度转向(US/OS)梯度:
稳定性因子A代表了稳态转向对车速的依赖程度,不足/过度转向梯度U则代表了稳态转向对侧向加速度的依赖程度。U和A的关系为:
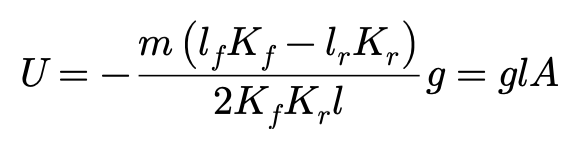
如果轮胎的侧偏特性为线性,则稳态转向车辆的侧向加速度与转向角之间的关系转换为:
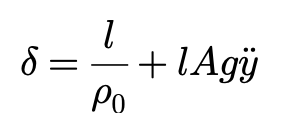
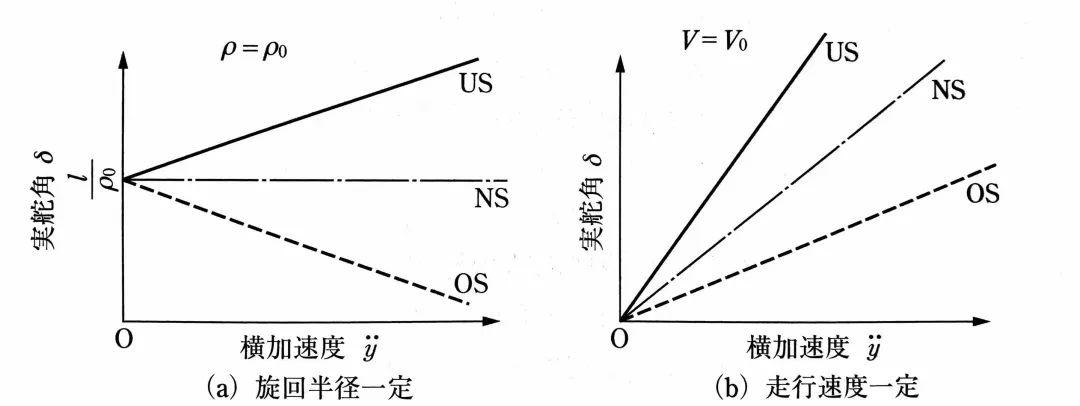
左图为恒定转向半径,右图为恒定车速条件下,具有线性轮胎的车辆,其侧向加速度与所需转向角之间的关系。
从U的定义出发,还可以将U写作:
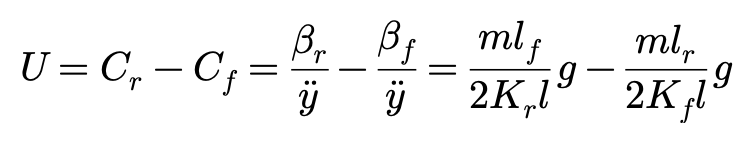
Cf和Cr分别被定义为前后轮胎的转向变形,即稳态转向的侧偏角除以侧向加速度。
上式正好与第四节末尾给出的形式一致,给出了同样的概念:稳定性因子是稳态转向时单位侧向加速度下的前后轮侧偏角之差。
最后,我们汇总了稳态转向条件下的转向特性。
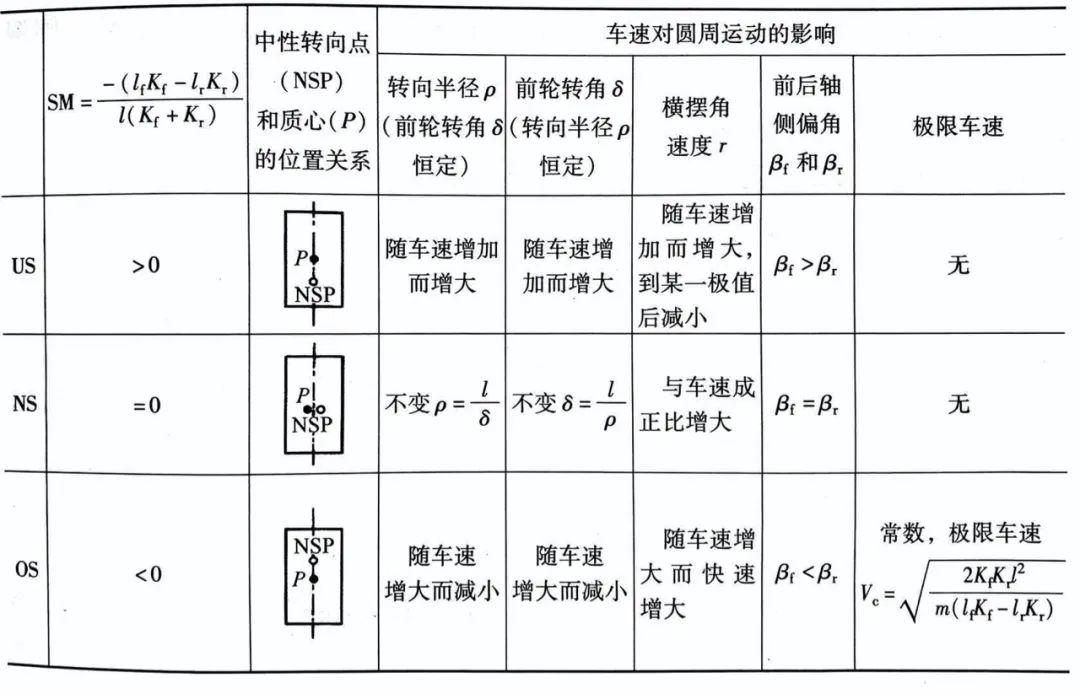
陆
稳态转向与轮胎非线性
如前文所述,车辆的侧偏力可能与其侧偏角不成正比。在侧偏角较大或其他某些条件下,轮胎侧偏力会表现出非常线性的特征。
汽车在稳态转向运动中,前后轮垂直载荷与对应的侧偏力之比等于质心的侧向加速度。因此有:
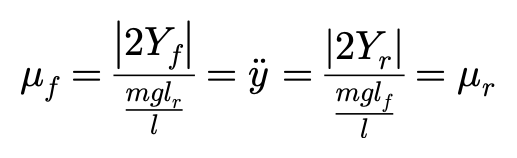
如果继续假设,由轮胎侧偏角引起的侧偏力是仅有的侧向力,则μf和μr分别仅由βf和βr决定。如果前后轮的侧偏特性,以及车辆质心的侧向加速度是已知的,则能够马上求出前后轮的侧偏角βf和βr的大小。
来看一个具体的例子:
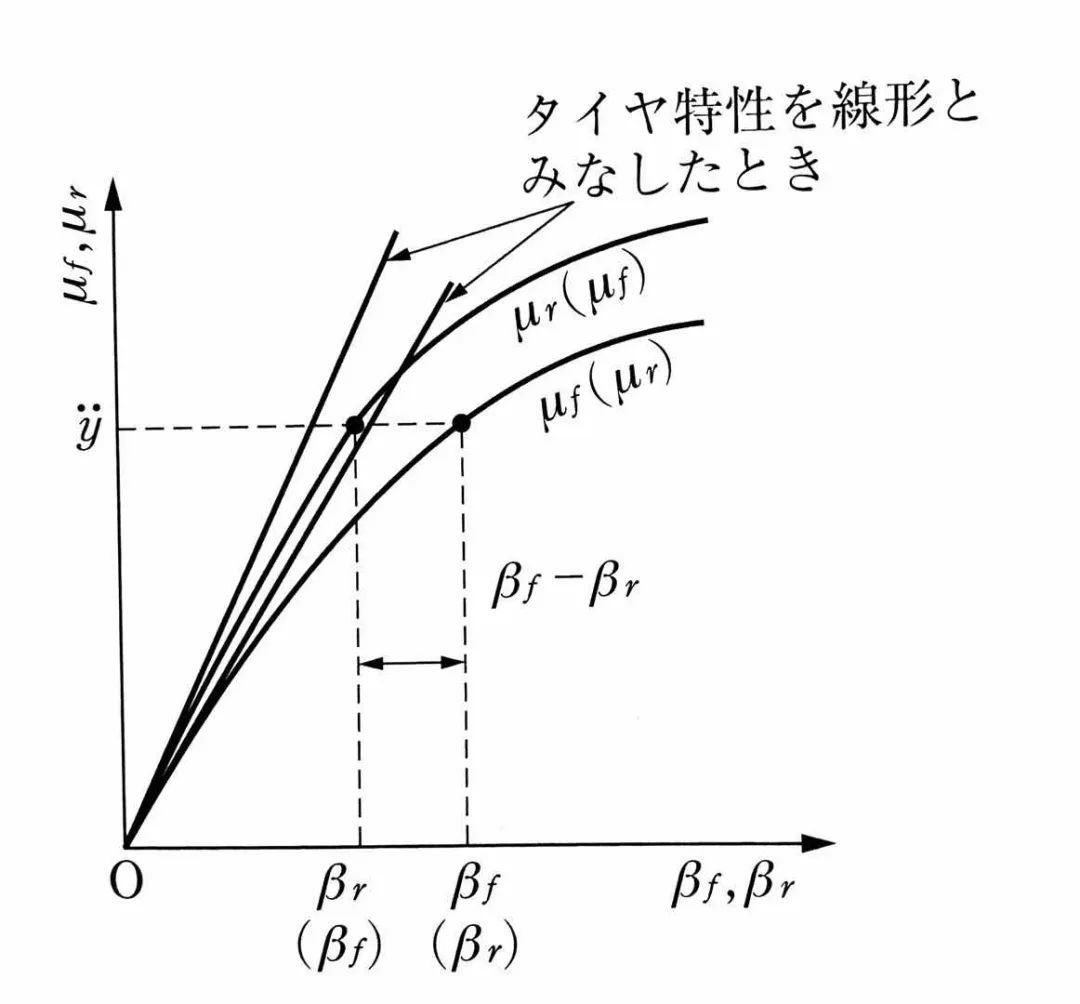
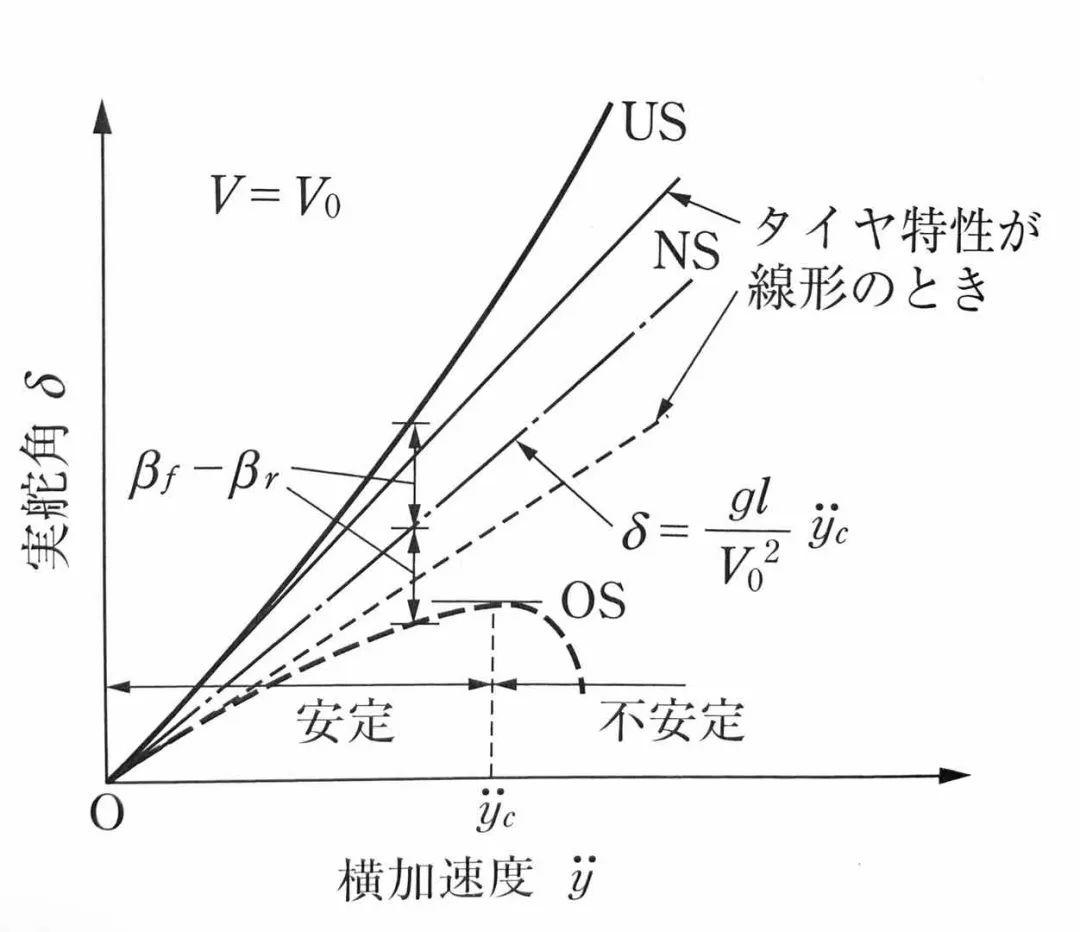
当轮胎的侧偏特性为非线性时,前后轮的侧偏特性可以用上图的曲线来表达。如果车辆做稳态转向,则侧向加速度y”与μf和μr相等。所以,只要知道了侧向加速度y”,就可以根据侧偏特性曲线得到βf和βr的值,从而求得βf-βr的差值。从图上可以看出:
-
如果μf<μr,则βf>βr,因此车辆呈US特性
-
如果μf=μr,则βf=βr,因此车辆呈NS特性
-
如果μf>μr,则βf<βr,因此车辆呈OS特性
车辆在稳态转向过程中,无论前后轮上的侧向力是否与侧偏角成正比,以下几何关系都满足:
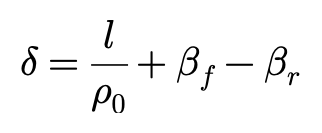
车辆以恒定转向半径做稳态转向时,侧向加速度y”和前轮转向角δ之间的关系可以表达为下图:
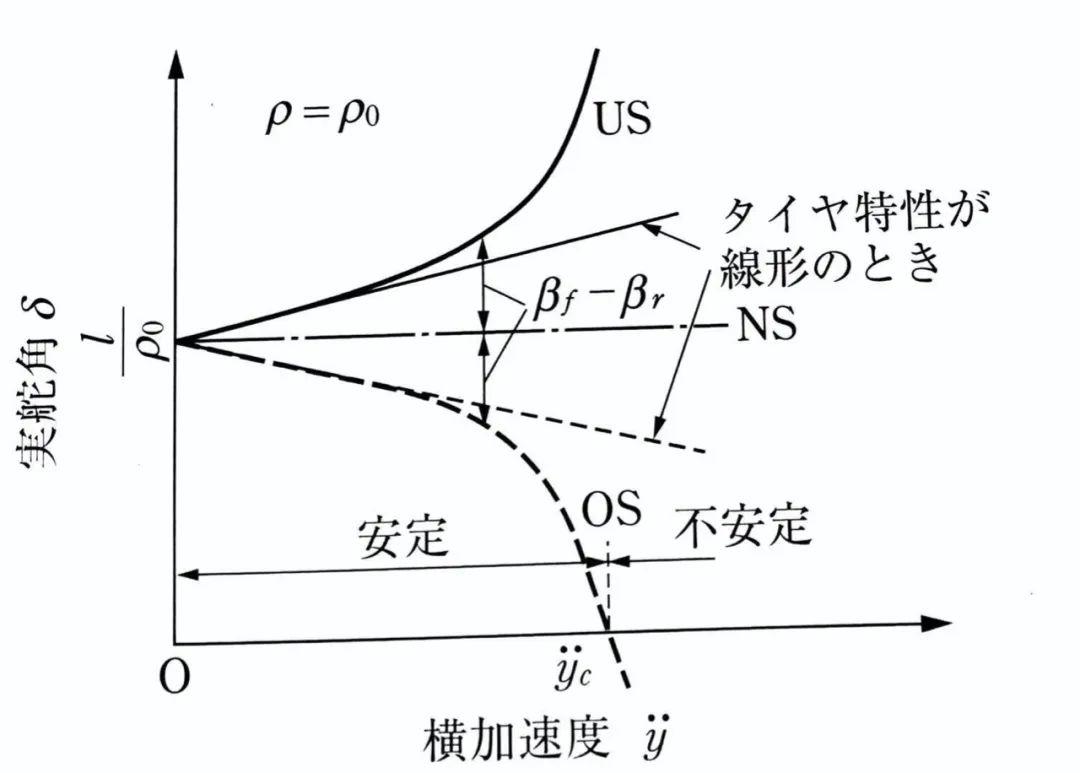
对于呈US特性的车辆而言,如果y”和轮胎侧偏角β都很小,则βf>βr,βf-βr为正,且几乎与y”成正比。当y”超出某一范围时,βf-βr与y”将不再成正比(图上的直线为轮胎特性为线性时的情况)——而是转向角δ随着y”的增加而迅速增大,车辆表现出很强的US特性。
与此相反,在车辆呈OS特性的情况下,当y”增加并超出某个范围时,将表现出很强的OS特性。继而转向角δ迅速减小,当y”=y”c时,转向角δ=0——这意味着:作为半径为ρ0定圆运动,具有OS特性的车辆,想通过提高其车速的办法来增大其侧向加速度,是不可能的。
即便不存在轮胎非线性因素的影响,转向角δ=0的y”c值仍然是存在的——只是比非线性的情况要大得多。
我们继续来看车辆以恒定速度V=V0做圆周运动的情况。这时的几何表达式可以写作:
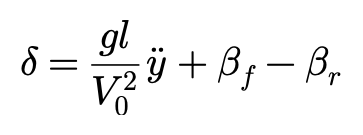
这里y”是已知的,βf-βr的值可以利用侧偏特性计算出来,利用上面的方程,可以得到车辆的前轮转向角与其侧向加速度y”之间的关系,
图上可以发现,当车辆呈现US转向特性时,转向角δ与侧向加速度y”几乎成正比增加,当y”达到某一特定值后,更呈现出明显的US特性。
当车辆呈OS转向特性时,y”很小的时候,转向角δ也随y”成比例增加,但当y”达到某个特定值后,转向角δ也随y”的增长变弱,当y”=y”c时,转向角δ达到峰值。当y”>y”c,转向角δ会逐渐减小。
转向角δ减小,会让恒定速度下的回转半径变小,这表明车辆向右转的话,应该往左打方向——这在现实中时不成立的,没有实际的物理意义。因此对于y”>y”c,以更小的转向半径做圆周运动是不可能实现的。
对于呈OS特性的车辆而言,不论车速如何,可以实现的转向半径总有一个下限。
现实世界中的轮胎侧偏特性比我们认为的要复杂的多。在实际应用当中,我们还要考虑更加极端的情况——比如前后轮胎侧偏特性交叉的情况。
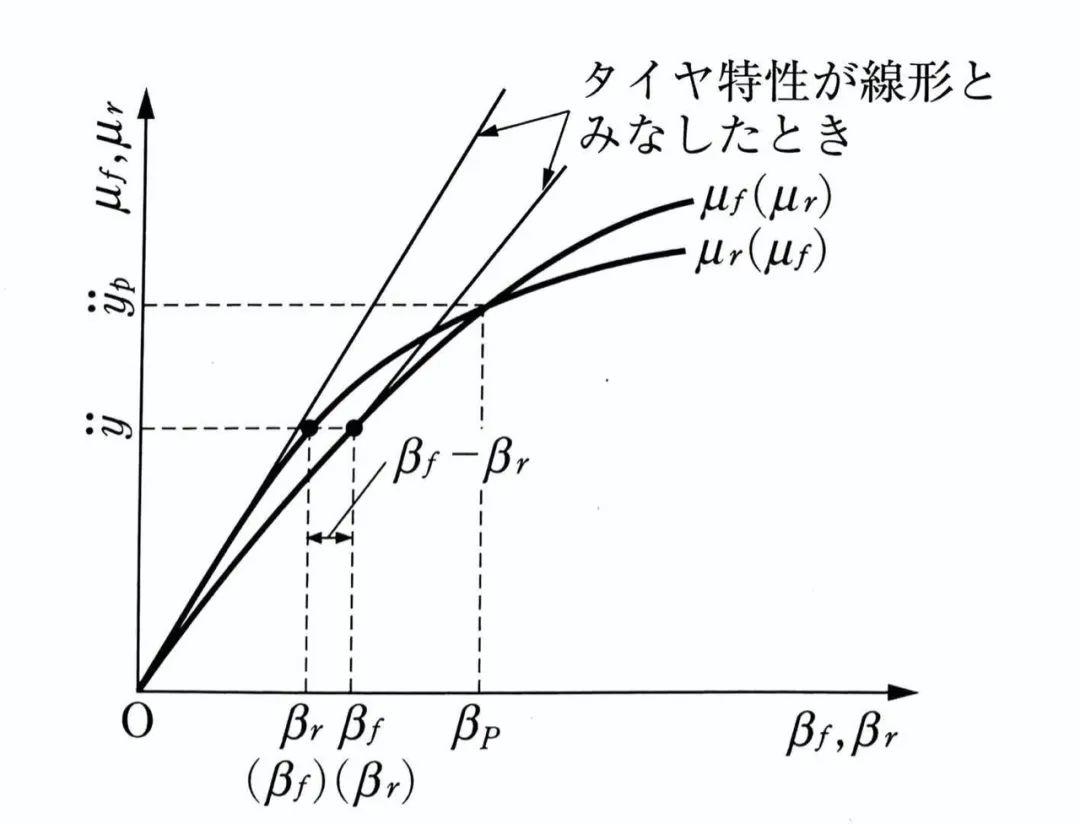
A情形:
-
如果βf和βr都小于βp,则μf<μr
-
如果βf和βr都大于βp,则μf>μr
B情形:
-
如果βf和βr都小于βp,则μf>μr
-
如果βf和βr都大于βp,则μf<μr
继续做图,来看定圆运动下车辆转向角和侧向加速度之间的关系:
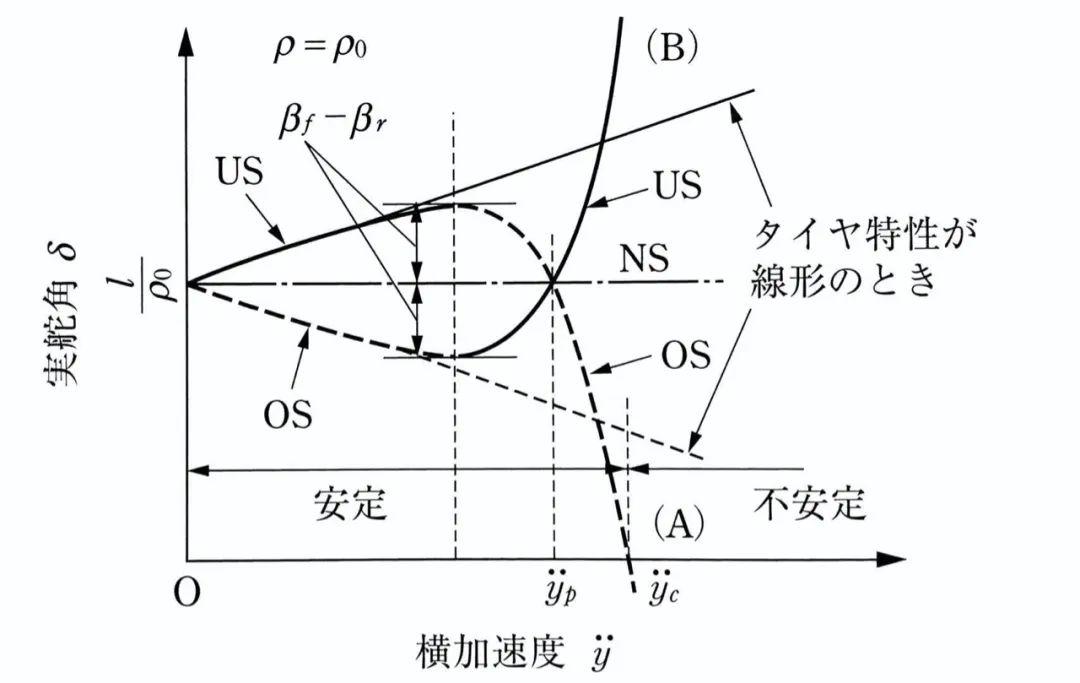
可见,受到交叉性的影响,OS特性在交叉点之后转变为US特性,US特性转变为OS特性。
恒定车速下,车辆转向角与侧向加速度之间的关系,US和OS特性逆转:
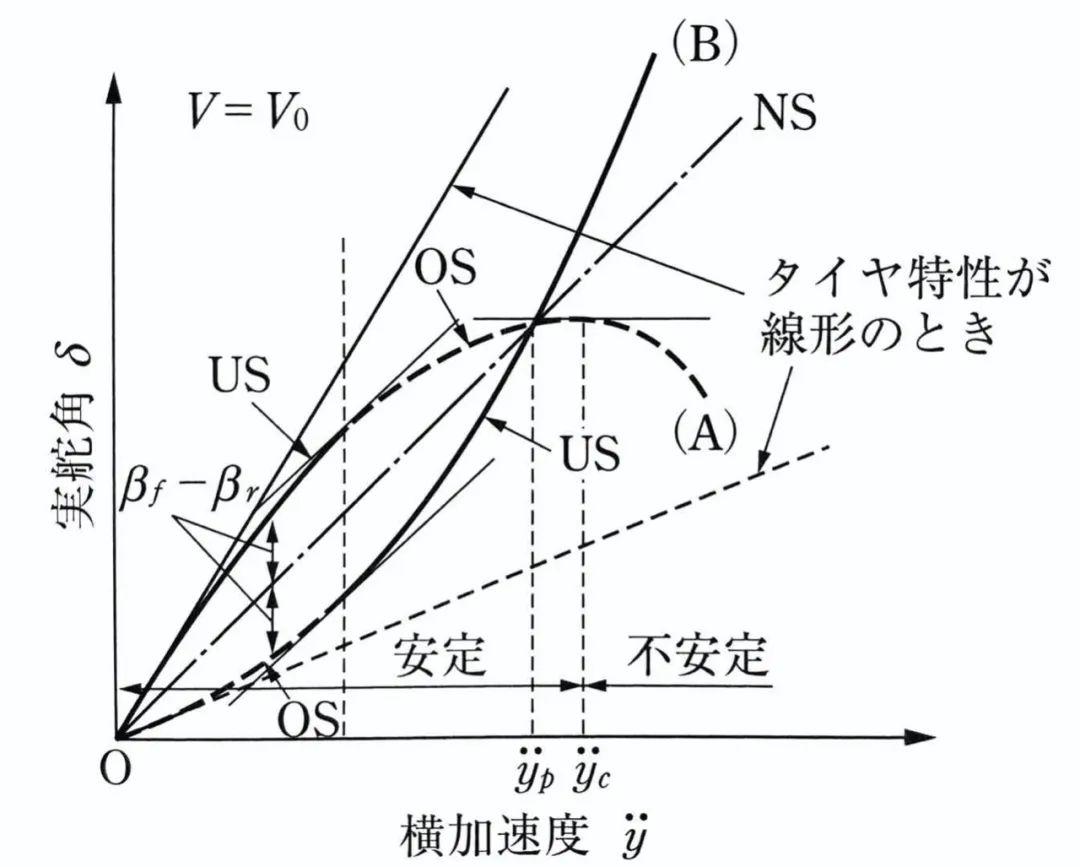
这种由于侧向加速度y”的改变而导致车辆转向特性的改变,被称作逆转向特性。
-
如果βf和βr都小于βp,则μf<μr
-
如果βf和βr都大于βp,则μf>μr
在如上的A情形下,随着侧向加速度的增加,车辆呈现明显的OS特性,从而变得静态失稳,后轮比前轮先到达极限,这种状态就被称作车辆的甩尾或车辆的侧滑。
-
如果βf和βr都小于βp,则μf>μr
-
如果βf和βr都大于βp,则μf<μr
在如上的B情形下,随着侧向加速度的增加,车辆呈现明显的US特性,不管转向角多大,车辆都不能以超过特定值的侧向加速度做圆周运动,这种状态就被称作车辆的犁地效应。
如果前后车轮同时到达侧向力的上限,这种状态就被称作车辆的漂移。
柒
车辆的动态特性
了解了车辆的静态特性——即车辆的稳态特性之后,我们将焦点转向车辆的动态,从而学习关于车辆运动特性方面的知识。
在动态的领域当中,研究的内容分为四个方面,包括:
-
车辆对转向输入的瞬态响应
-
转向输入响应的传递函数和响应时间历程
-
车辆对与周期性转向输入的响应
-
非线性轮胎特性的影响
就让我们分别来看。
车辆对转向输入的瞬态响应和方向稳定性,固有频率,阻尼比,响应性
开篇第一章当中,我们推倒出了动力学系统的运动方程,并在线性假设前提下,通过拉普拉斯变换得到特征方程:
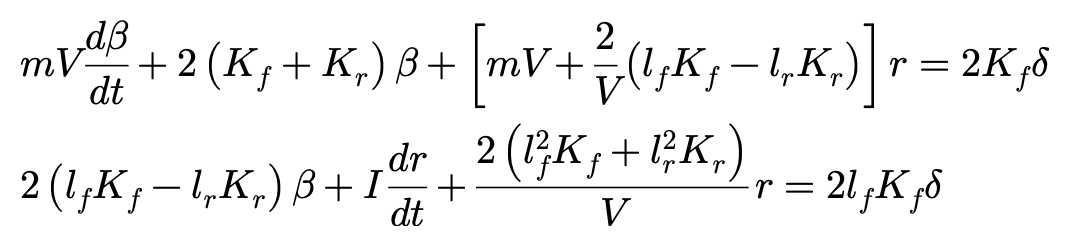
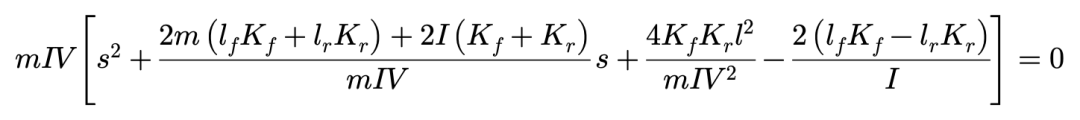
为了理解该动力学系统的瞬态响应,我们有必要考察该特征方程的根。以上特征方程,可以简化形式为:
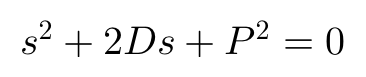
其中:
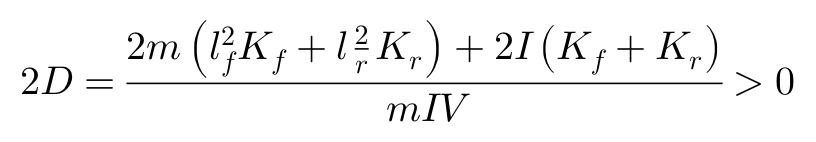
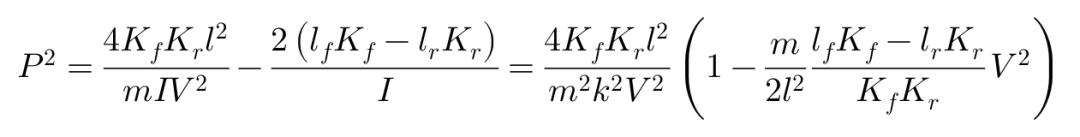
I为车辆的横摆转动惯量,k为车辆横摆力矩半径。
对于形式为:
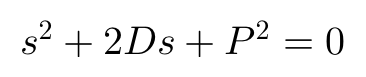
的特征方程来说,其响应可以表示为:
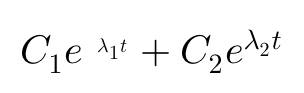
其中,λ1和λ2是特征方程的根:
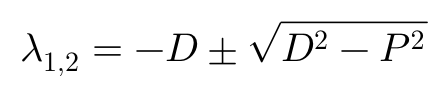
至此,我们的关注点,变成了特征方程根的特性——即λ1和λ2到底是实数还是复数——这决定了系统的瞬态相应特性及其稳定性。具体地说:
-
当D^2-P^2>=0,P^2>0时,λ1和λ2为负实数,瞬态响应作无震荡衰减(系统稳定)
-
当D^2-P^2<0,P^2>0时,λ1和λ2为复数,如果其实部为负,瞬态响应作震荡衰减(系统稳定)
-
当P^2<0时,λ1和λ2一个为负实数,一个为正的实数,瞬态响应为非震荡发散(系统不稳定)
需要注意,发生以上情况的前提是:这辆的转向输入是预先给定的,并不随车辆的状态而改变——这是一个非常苛刻的条件,在日常驾驶情况下不容易满足。汽车并不会始终以这样的方式被操控,因此,驾驶员的操作方式对车辆的稳定性起到了关键性的作用。
有了以上三种情形的分类,我们就可以研究什么样的车辆,在什么场合下会呈现出三种情况下的运动特性。
首先来看第三种情况。
此前关于静态裕度(Static Margin)的讨论,有以下方程:
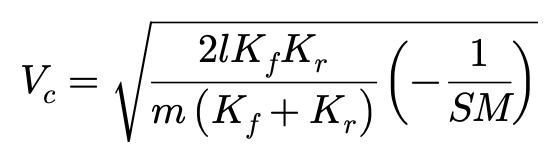
对于所有大于Vc的车速,P^2<0总是成立的,于是这被称作是力学系统的静态不稳定条件。
如果车辆呈现转向过度OS的特性,当车速为Vc时,车辆的侧向运动将变得不稳定,即对于一固定的转向输入,车辆的运动会呈现非震荡发散。
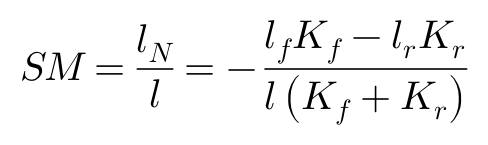
这一稳定性界限就由静态裕度SM决定,如果你还记得,SM与系数lfKf-lrKr又有着千丝万缕的联系。
总体来说,SM的绝对值越小,前后轮的总侧偏刚度越大,则稳定性临界车速Vc就越大。
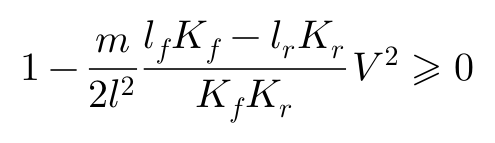
上面这个得出稳定性临界车速Vc的车辆稳定性条件方程,正是决定P^2项符号的表达——只要V<Vc,车辆就是稳定的。
从这个方程当中,还有另外一个有趣的发现:要让车辆处于稳定状态,前后轮的侧偏刚度应分别具有上限值和下限值。
证明也很简单,将上述不等式改写成:
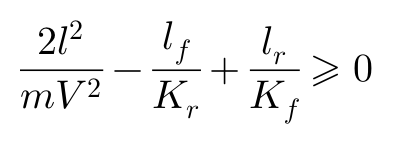
于是,前轮刚度的上限为:
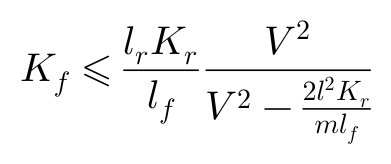
后轮刚度的下限为:
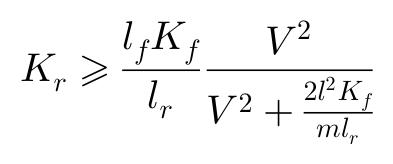
画图表达如下:
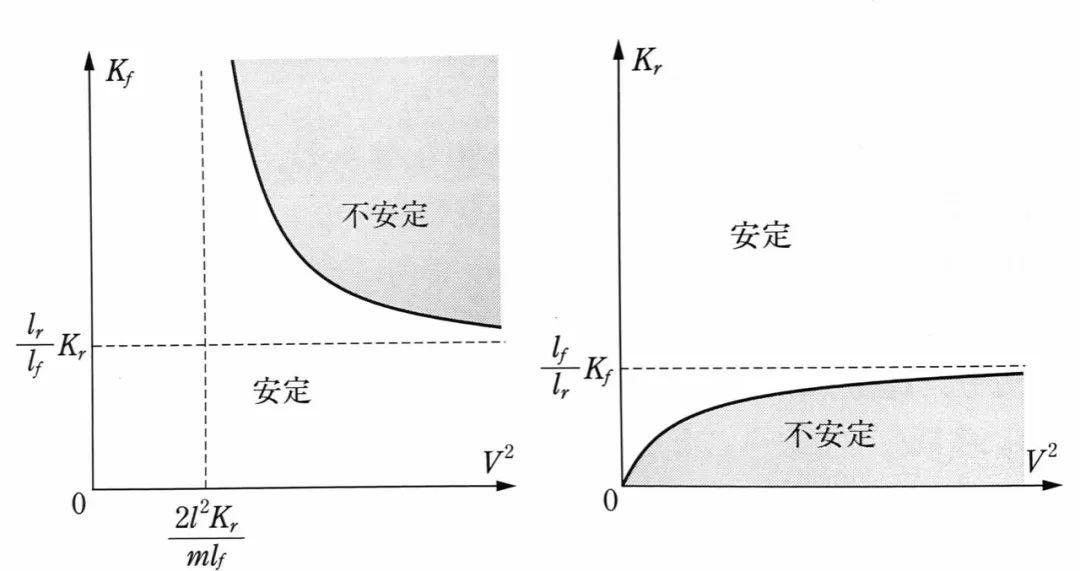
再来看系统稳定的前两种情况:
如果系数lfKf-lrKr<0,车辆呈现转向不足US特性;或虽然车辆表现为过度转向特性OS,但V<Vc。这两种情况下,P^2总是大于零,因此车辆的运动就是稳定的。
P^2大于零,我们就可以重点来看D^2-P^2的表达:
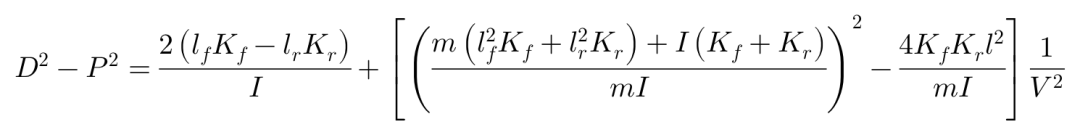
这个表达式可以得出很多有趣的结论:
-
当第一项中的lfKf-lrKr大于等于0,那么多项式也会大于等于零。这代表:车辆的稳态转向特性,不管是过度转向OS还是中性转向NS,无论车辆对于转向输入的瞬态响应是否稳定,都总是非震荡的。
-
当第一项中的lfKf-lrKr小于0,则多项式的值取决于V,当超出某一车速Vc后,多项式的值由正变负。这代表:当车辆呈转向不足特性US时,在车速低于某特定车速时,车辆对转向输入的瞬态响应表现为非震荡的形式;一旦高于某特定车速,响应将表现为震荡。
经过计算,可以得出当SM>0(即lfKf-lrKr>0,车辆呈现转向不足特性US)时,对转向输入响应从非震荡变为震荡的临界车速Vs:
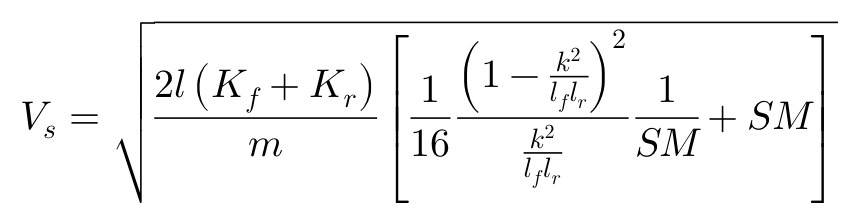
公式当中,Vs受横摆转动惯量(k^2/lflr)的影响,当其=1时,Vs达到最小;当其大于或小于1时,Vs都会增大。
这是说:当车辆的横摆转动惯量大于或小于某一定值时,车辆对转向输入的响应由非震荡向震荡变化的速度总是会增加;并且Vs又一个最小值,此时的静态裕度SM可以表达为:
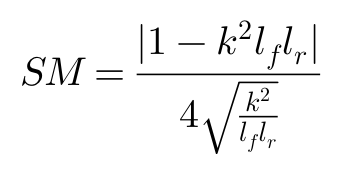
这意味着,车辆对转向输入的瞬态响应特性与车辆行驶速度和转向特性尤为相关。
于是,我们有了下面这张图,来自《Beyond the Apex》:
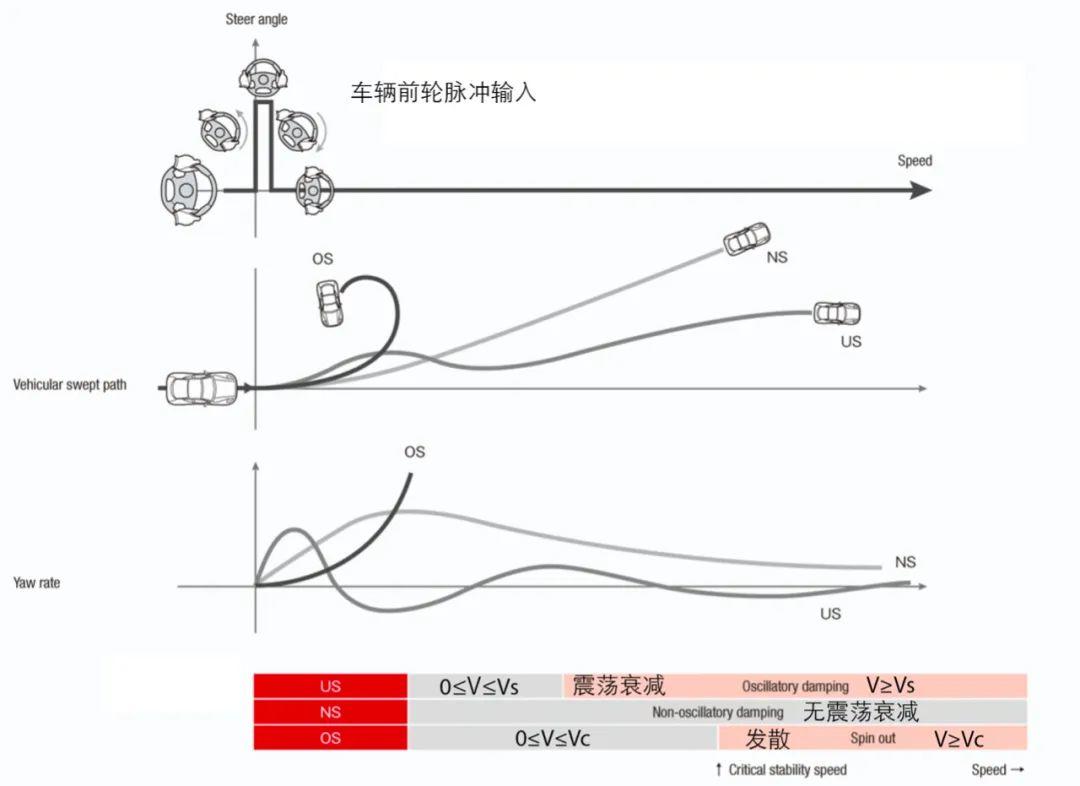
再来研究车辆对转向输入响应的固有频率ωn和阻尼比ζ。
从特征方程:
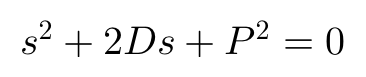
得到特征方程的系数:
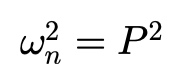
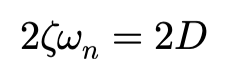
固有频率ωn和阻尼比ζ用静态裕度SM表达:
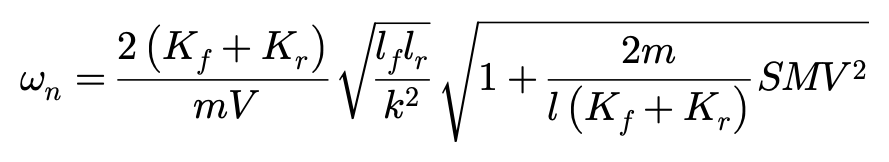
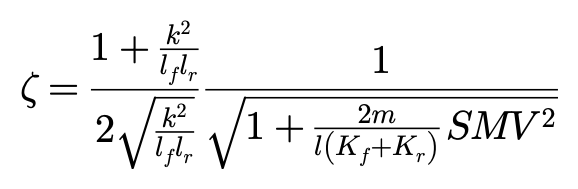
有了方程,我们就可以研究车辆的固有频率和阻尼比随车辆的转向特性和行驶速度变化的规律。
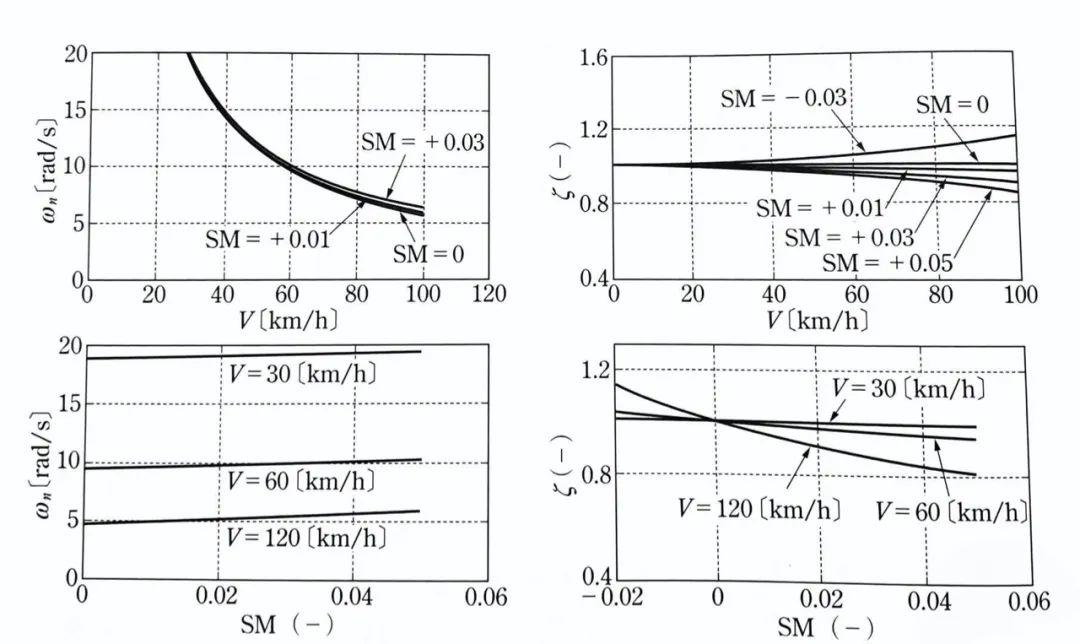
左边的两张图可以看出,固有固有频率ωn明显随着车辆行驶速度V增大而减小,但它仅随着静态裕度SM的增加而略有增加。
右边的两张图可以看出,随着静态裕度SM的增加,阻尼比ζ减小,从而导致车辆对于转向输入的响应愈加震荡。
另外,当车辆呈现转向不足特性US时,阻尼比ζ随车速的增加而减小,车辆运动变为小阻尼运动,从而引发更多的震荡。当车辆呈现转向过度特性OS时,阻尼比ζ会随着车速的增加而增加,从而使车辆对转向输入的响应恶化。
再来看响应性。
对稳定的线性系统而言,设其特征方程的特征根的实部为λ,则下面公式定义的响应时间就是表示其系统响应速度的一个参数:
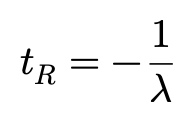
因此当D^2-P^2≥0时,tR为:
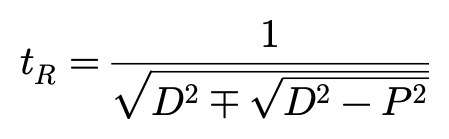
当D^2-P^2<0时,tR为1/D
继续带入SM,可以得到:
当D^2-P^2≥0时:
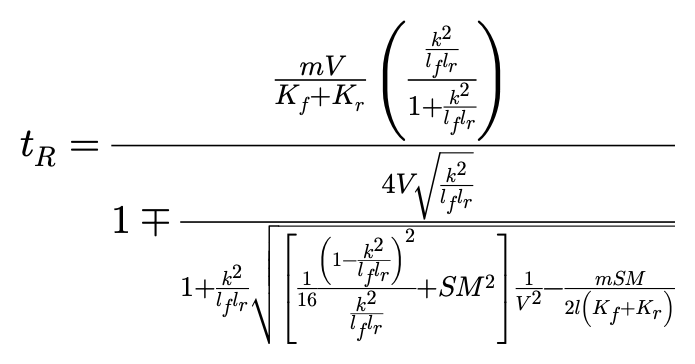
当D^2-P^2<0时:
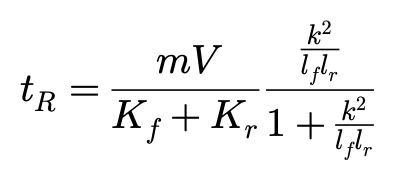
一般来说,大多数情况下,都有:
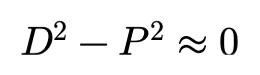
此时,其上面的两个方程相等,于是就可以采用后者:
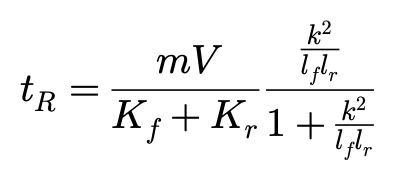
这个方程作为标准的车辆响应时间tR的估算公式。
由上面的讨论,我们可以总结,车辆动态特性的基本性质(固有频率ωn,阻尼比ζ,响应时间tR)取决于车辆的行驶速度V和以静态裕度SM衡量的转向特性。
如果lf≈lr,且Kf≈Kr,则车辆质量与轮胎侧偏刚度之比为m/(Kf+Kr),轴距l以及由轴距和车辆质心位置决定的横摆转动惯量k^2/lflr也影响着瞬态响应。尤其值得注意的是,正是横摆转动惯量k^2/lflr的形式真正地影响着车辆的动态性能。
转向输入响应的传递函数和响应时间历程
刚刚,我们通过研究特征方程和特征根,间接地对车辆的转向输入的瞬态响应特性做了了解,现在,我们需要通过更直接的求解描述车辆运动的基本方程获取更多的信息。
对第一节的车辆运动方程进行拉普拉斯变换后,纳入固有频率ωn,阻尼比ζ的表达,对β(s)和r(s)求解代数方程,可以得到:
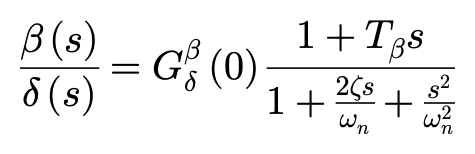
上面这个表达是侧偏角β对转向输入δ的传递函数。
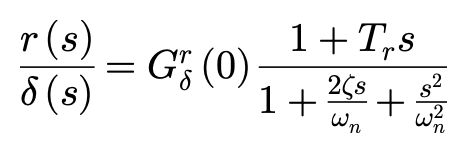
上面这个公式是横摆角速度r对转向输入δ的传递函数。
其中:
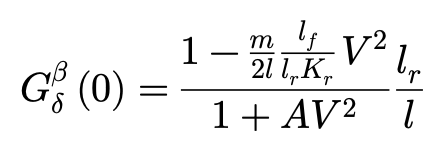
这个表达被称作车辆质心侧偏角增益常数,是车辆作稳态转向时,其侧偏角β相对其转向角δ的稳态值。
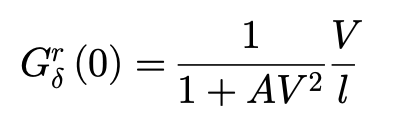
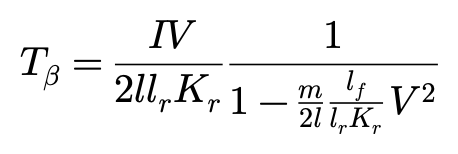
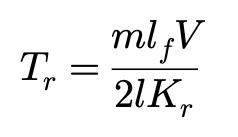
上面,我们获得了侧偏角β和横摆角速度r对转向角δ的拉普拉斯变换响应,下面我们可以通过反拉普拉斯变换,求出针对某给定的转向角δ,车辆的侧偏角β和横摆角速度r的响应。
直接给出计算结果,当车辆响应为无震荡的临界状态(阻尼比ζ=1时),有:
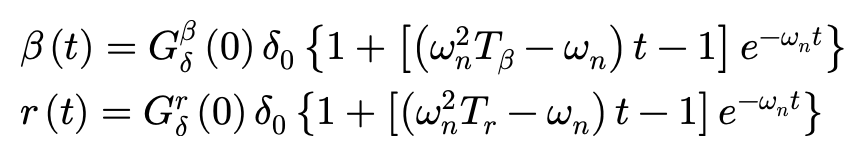
当车辆响应为有震荡时(即阻尼比ζ<1时),有:
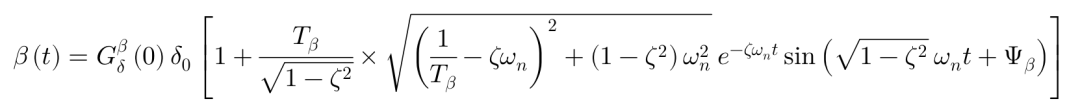
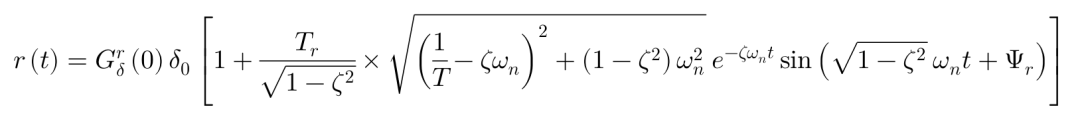
其中:
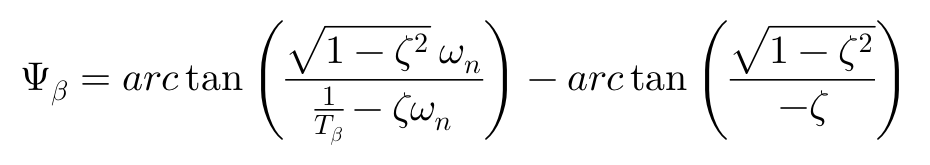
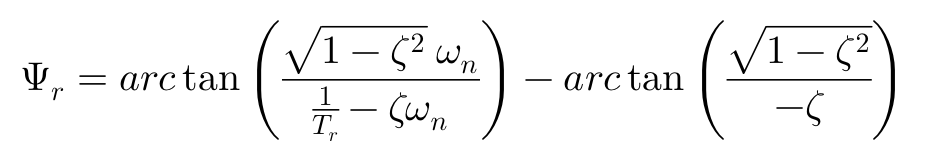
关于车辆对转向输入的响应性,除了上述解析计算之外,还可以用横摆角速度达到问态的时间te,以及达到第一个震荡峰值的时间tp来表示,如下图所示:
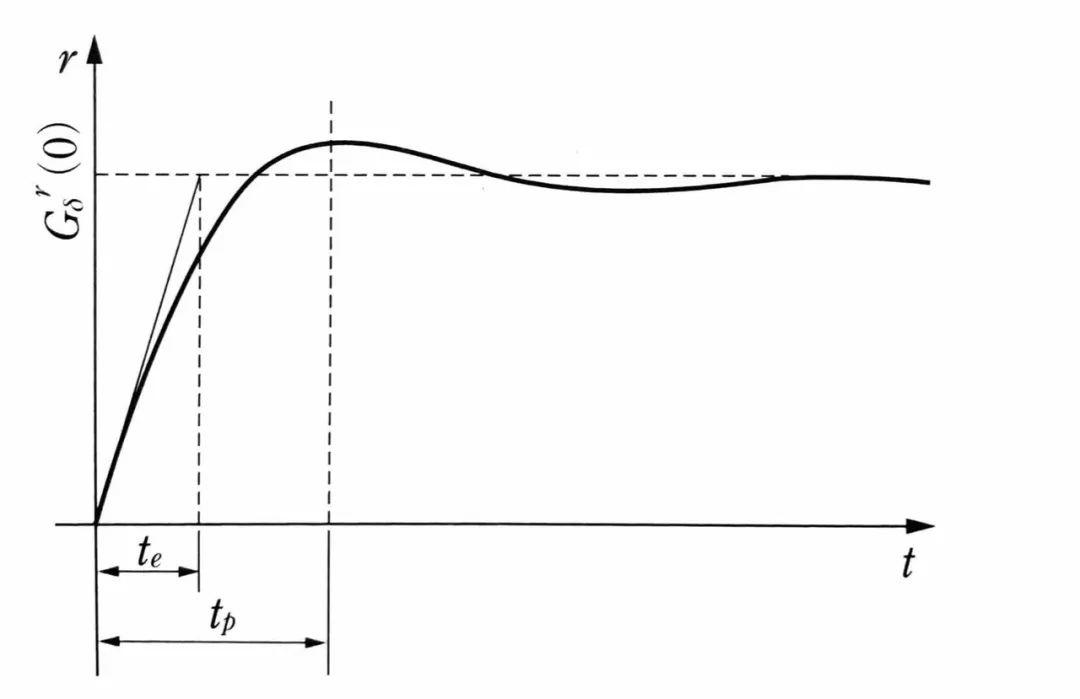
te和次tp的计算方法为:
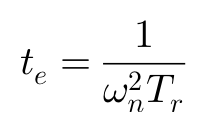
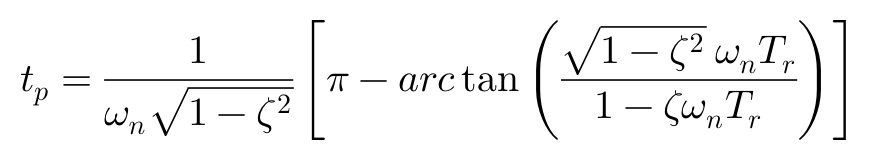
特别情况下,可以用tp来近似表示横摆角速度的响应时间。
车辆对于周期性转向输入的响应
在研究机械系统的动态特性时,通常离不开分析系统对周期性输入的响应。
对于振动系统,这被称作受迫振动;
对于控制理论,这被称作频率响应。
因此,我们有必要研究一下这个普世的课题。
如果车辆以地面固定坐标系来描述,则可以对运动方程进行拉普拉斯变换,求取关于y(s)和的代数方程,这里的y代表侧向位移。方程为:
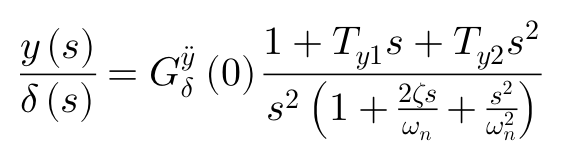
其中:
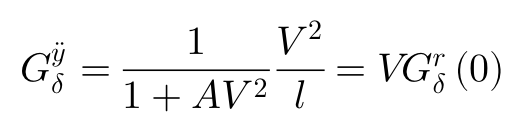
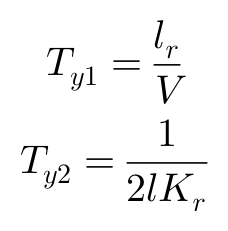
上面这个Gy”δ的表达被称作侧向加速度的增益常数,表示车辆稳态转向运动时,其侧向加速度对δ的响应。
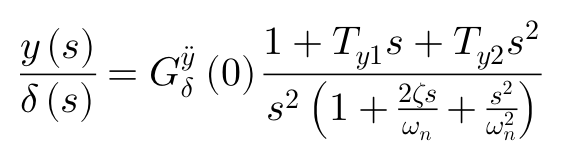
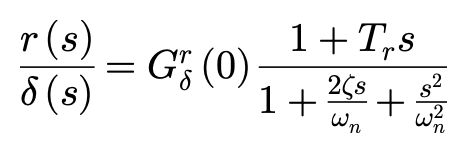
连列侧向加速度响应函数和横摆角速度响应函数,把s=j·2πf带入到以上两个方程并求解。
周期性转向输入δ下车辆质心处侧向加速度y”响应为:
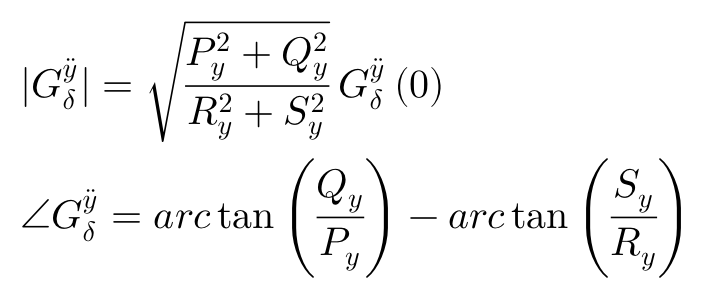
其中:
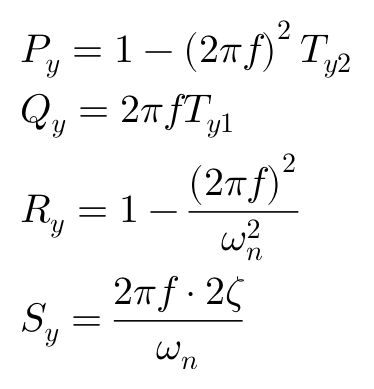
周期性转向δ下车辆横摆角速度r响应为:
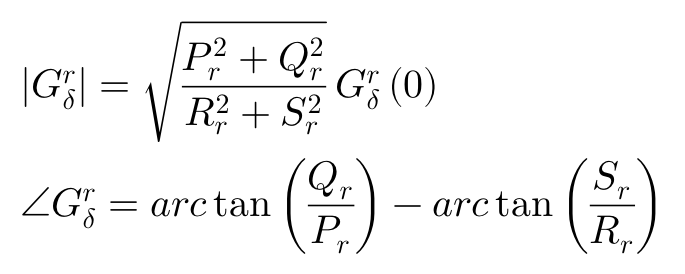
其中:
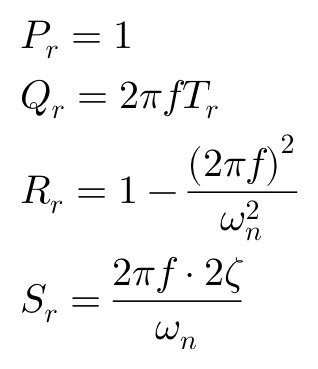
至此,我们可以定性地绘制出关于车辆横摆角速度响应的一般规律。在研究车辆固有的动态特性时,其横摆角速度对周期性转向输入的响应式我们最感兴趣的内容。图形如下,同样来自神作《Beyond the Apex》:
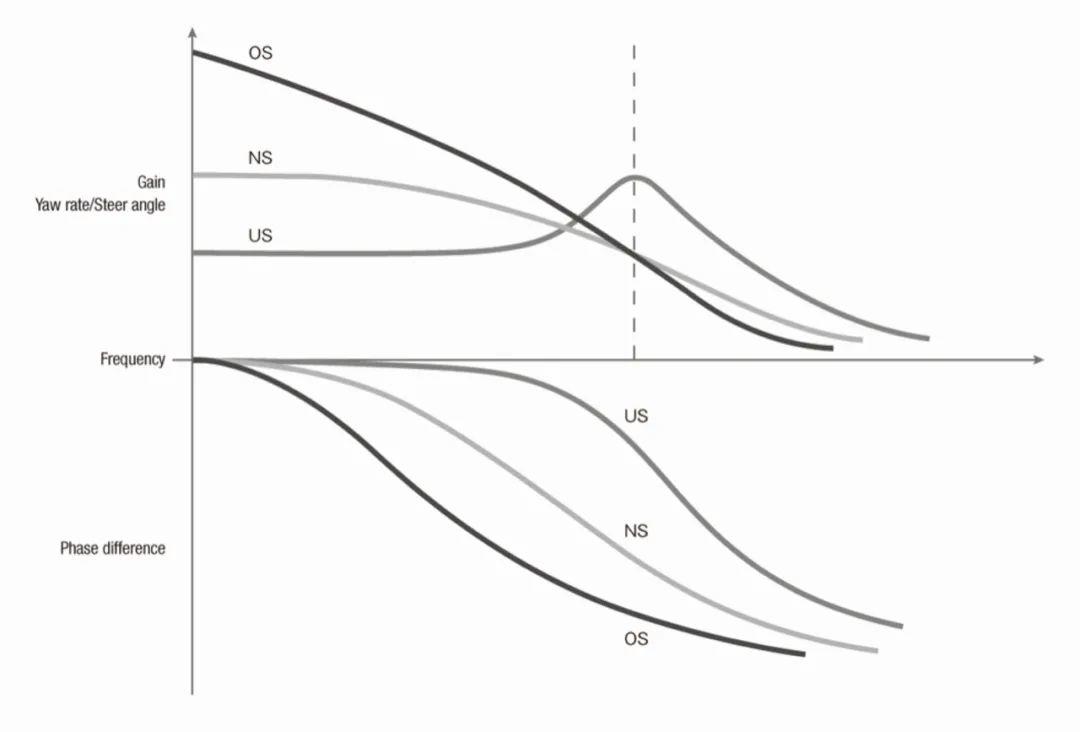
图上可以看到,当转向输入的频率较低时,横摆角速度对转向输入的增益几乎为恒定值。
-
随着转向频率的增大,对于具有不足转向US特性的车辆而言,其增益在某一频率处达到峰值,然后下降。对于具有不足转向特性US的车辆而言,其横摆角速度增益的峰值发生在车辆瞬态响应相对某一固定转向发生震荡的时刻。该峰值会随阻尼比ζ的减小而增加。行驶速度V越大,此峰值就会越大。出现此峰值的频率接近于车辆的固有频率ωn。
-
对于具有过度转向特性OS和中性转向NS的车辆而言,其增益不存在峰值,而是随着转向输入频率的增加而减小。
再看相位。在低频率时,相位滞后接近零。但随着频率的增加,相位滞后会急剧增加。三种转向特性下的表现都是一样的,只是这种趋势对于具有过度转向特性车辆而言更加明显。
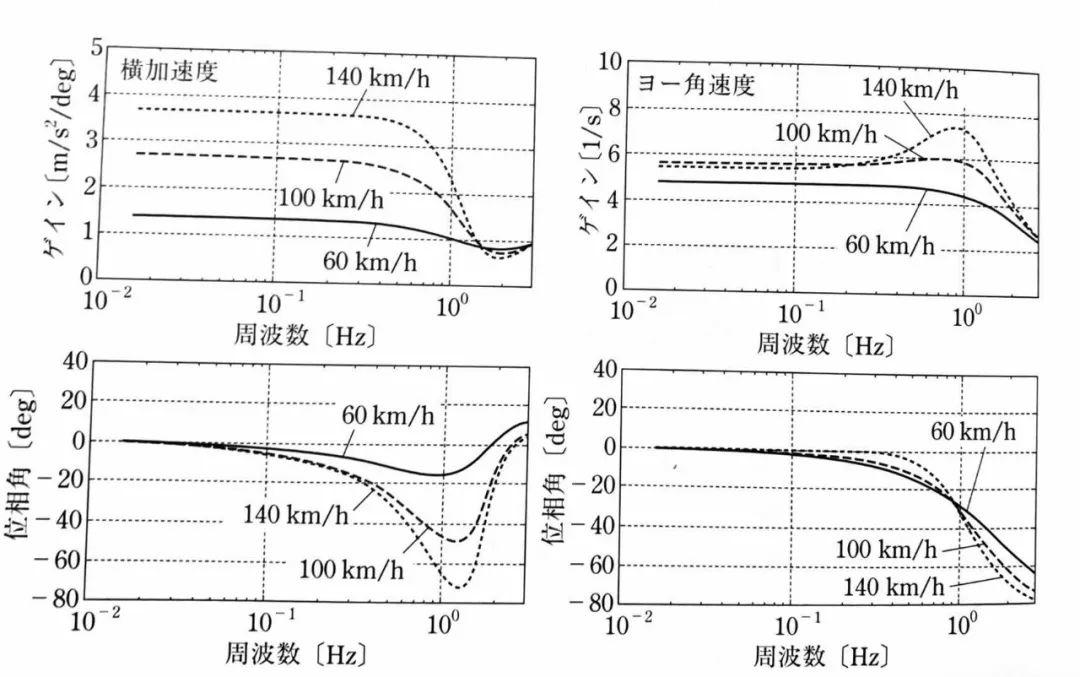
再来看一张图,这是一台小型轿车对周期性转向输入的横摆角速度r和侧向加速度y”响应的计算案例。
可以看到,随着车辆行驶速度的提高,在高频段的相位滞后角就会变大,尤其是对侧向加速度而言。进一步,由于这个实验车辆具备不足转向US的特性,因此横摆角速度响应增益的峰值出现在较高车速下,并且车辆的瞬态响应呈小阻尼震荡。
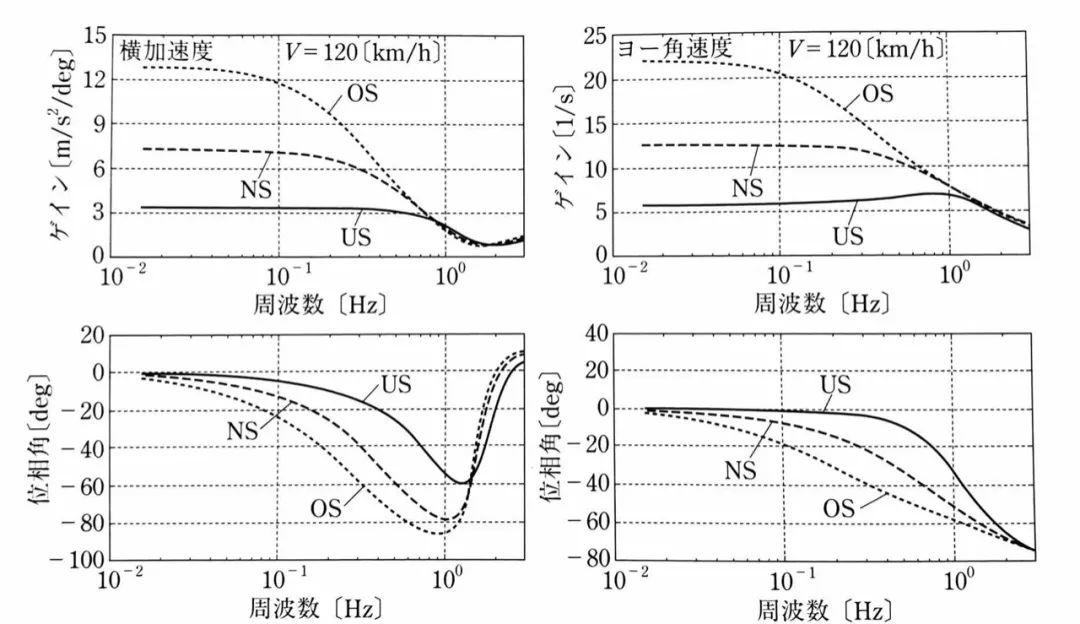
继续进行仿真,还能得到不同转向特性的仿真结果比较。图上显示的是侧向加速度和横摆角速度的频率响应曲线(增益&相位角)。
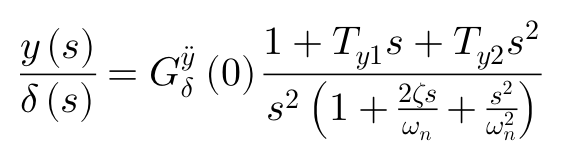
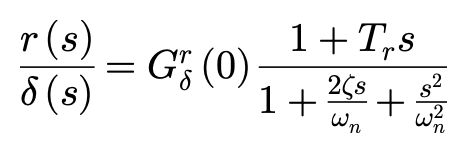
再次回顾侧向加速度和横摆角速度两个传递函数,可以发现:对转向输入δ而言,尤其是在高车速V条件下,与横摆角速度响应函数分子中s的系数(Tr=mlfV/2lKr)相比,侧向加速度响应函数中s的系数(Ty1=lr/V)较小。这就是为什么与横摆角速度r相比,尤其是在高速时,侧向加速度y”在相位上有很大延迟的原因。
那么,为什么侧向加速度响应函数中s的系数比较小呢?这是因为在计算侧向加速度响应函数时,横摆角速度与质心侧偏角的分子部分正好符号相反,互相抵消了。最终只剩下lr/V这一项作为侧向加速度传递函数分子s项的系数,并随着车速的增加急剧变小。
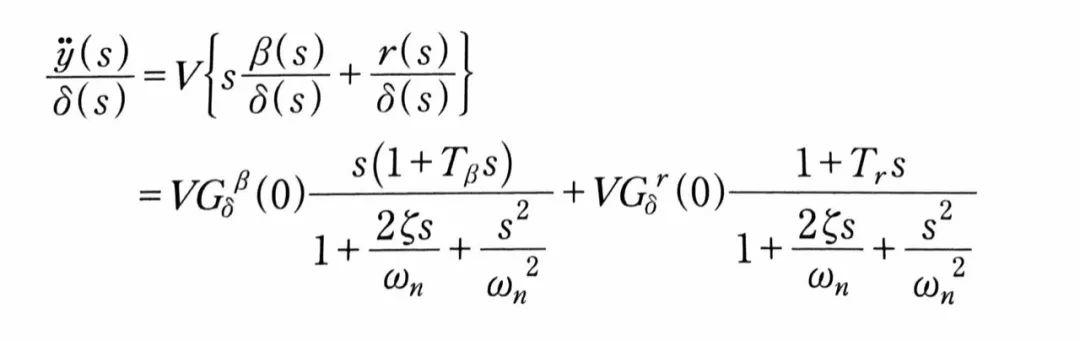
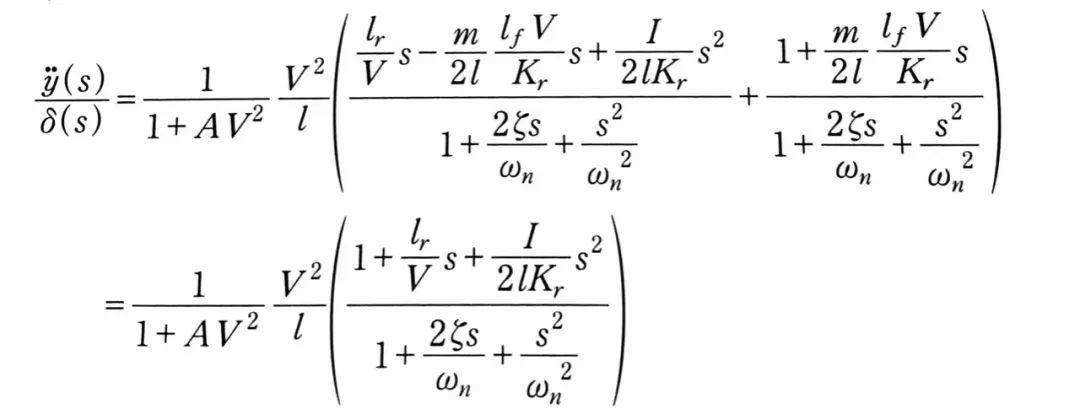
一般而言,传递函数中分子中s系数会对分母中s和s^2的系数造成的响应延迟产生重要的影响。
侧向加速度较大的延迟,是由于高速行驶时车辆会有一个反作用于转向角的侧偏响应——这是车辆动力学基本特性非常重要的一个特点。其原因就在于:侧向加速度y”与横摆角速度r之间,存在车辆侧偏运动的干预。
非线性轮胎的影响
轮胎侧偏力Y与侧偏角β之间有着紧密的联系,如果假设在β=0时,侧偏刚度为K,那么侧偏力达到饱和时的摩擦力μW可用β的二次多项式近似表达为:
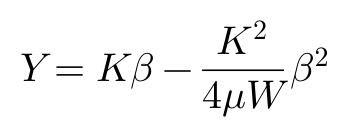
据此绘制下图:
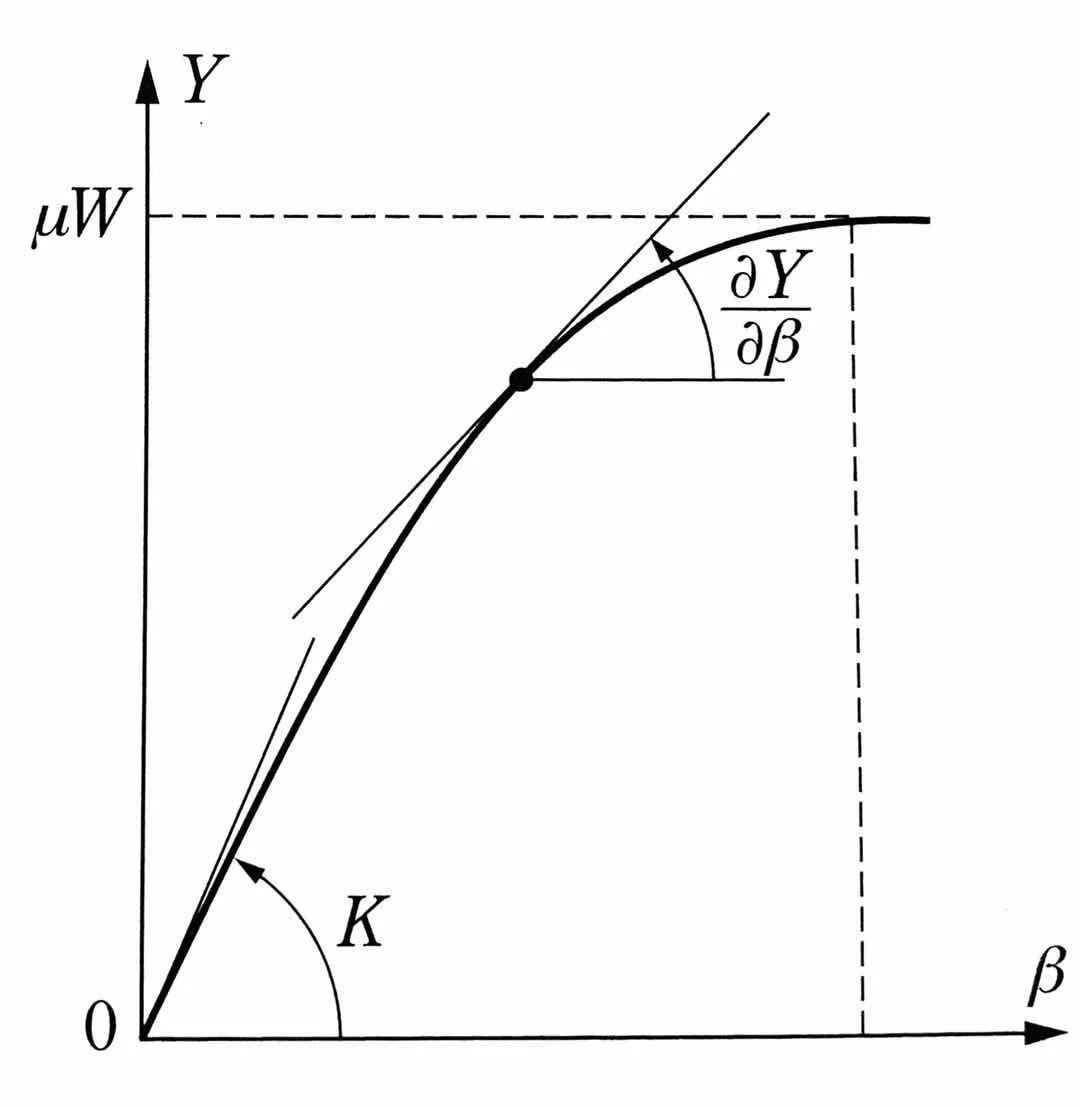
当一个重量为mg的车辆以侧向加速度y”作圆周运动时,作用于前后轮的侧向力为:
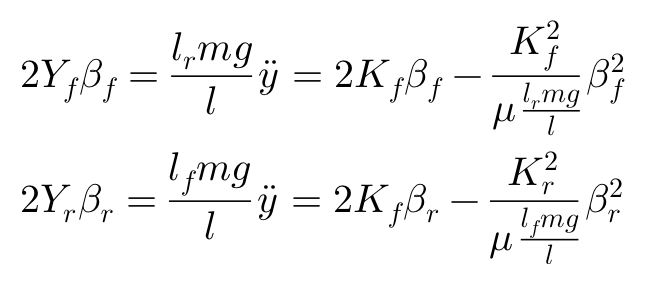
根据以上方程,可以求的等效侧偏刚度:
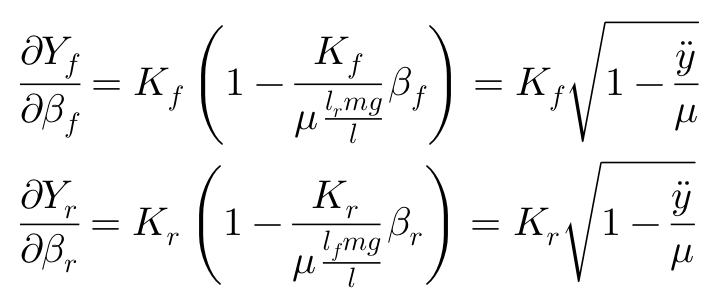
以上方程即为具有侧向加速度y”的圆周运动,在平衡点处,侧向力对侧偏角的梯度。如果y”/μ<<1,则可以简化为:
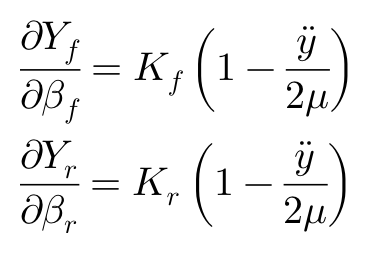
至此,当轮胎进入非线性特性区域内,其侧偏刚度Kf和Kr可由等效侧偏刚度(偏微分表达)替代。
在圆周运动中,车辆的侧偏刚度岁侧向加速度的增大而减小。当侧向加速度y”接近极限或接近路面与轮胎之间的摩擦系数μ时,侧偏刚度就会随着侧向加速度的增加而急剧减小。
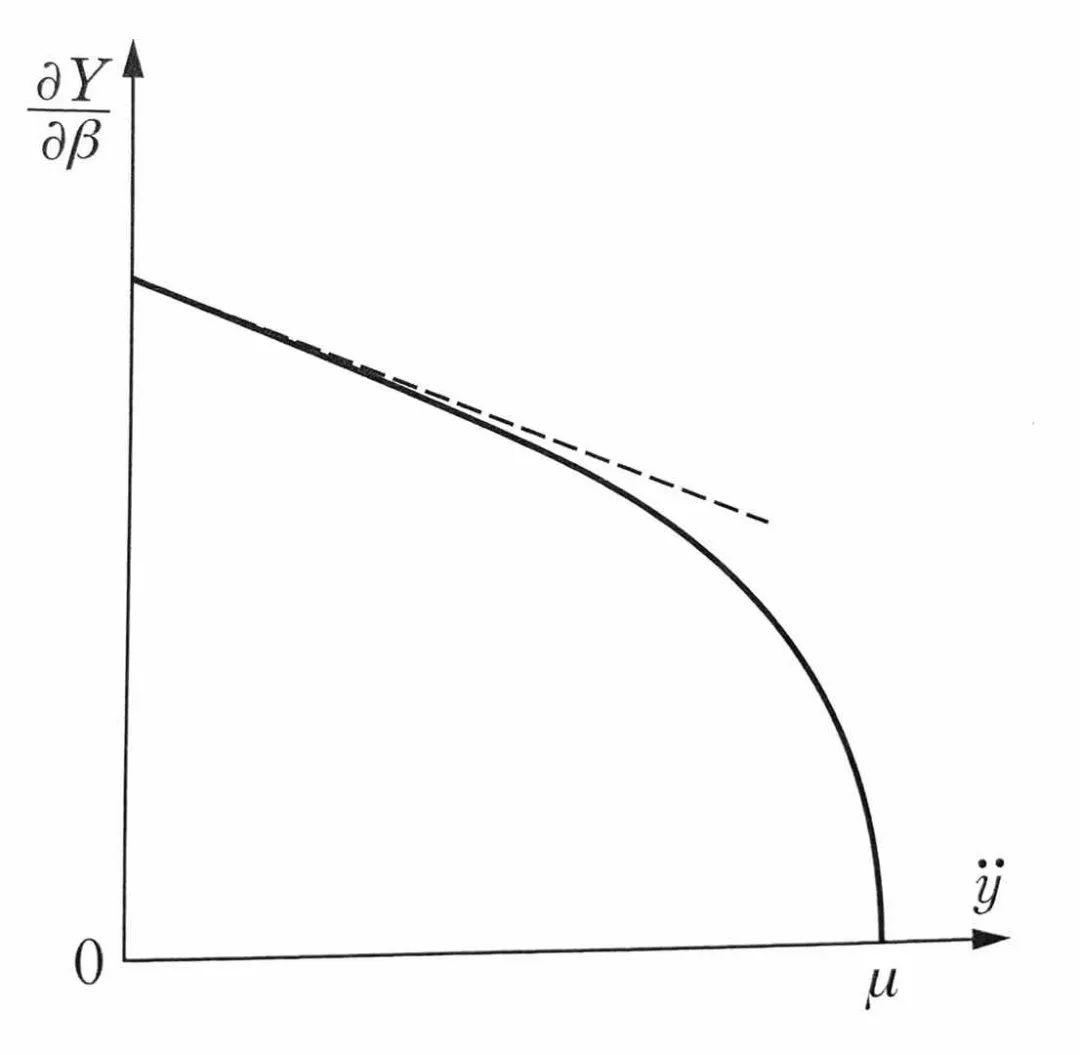
如虚线所示,在侧向加速度y”小于摩擦系数μ的范围内,可以认为侧偏刚度是线性减少的。
再来观察轮胎呈非线性时车辆的运动特性。在车辆作圆周并以侧向加速度y”运动时,由初始状态给定一个小转向输入,该时刻车辆所对应的小幅运动所代表的运动方程可以写作:
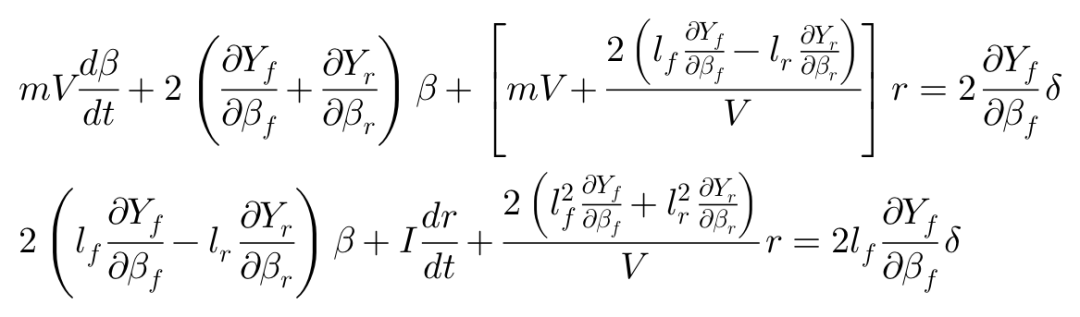
这就是轮胎呈非线性特性时,基于微摄动理论线性化后的车辆运动方程。
最后,我们把非线性情况的等效侧偏刚度(偏微分表达)替换原有的侧偏刚度,得到非线性条件下的动力学特性参数: 稳定性因子A*,固有频率ωn*及横摆角速度的响应时间te*如下:
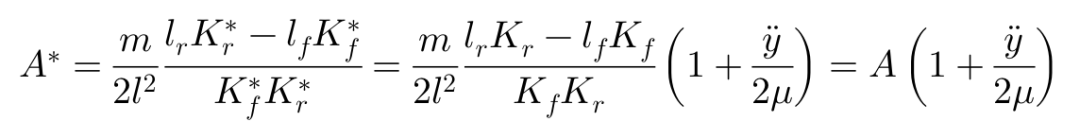
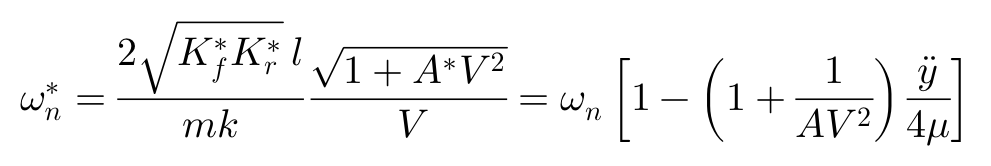
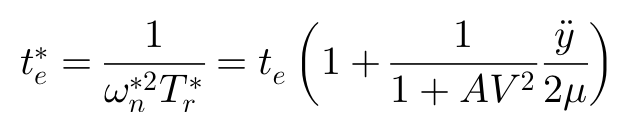
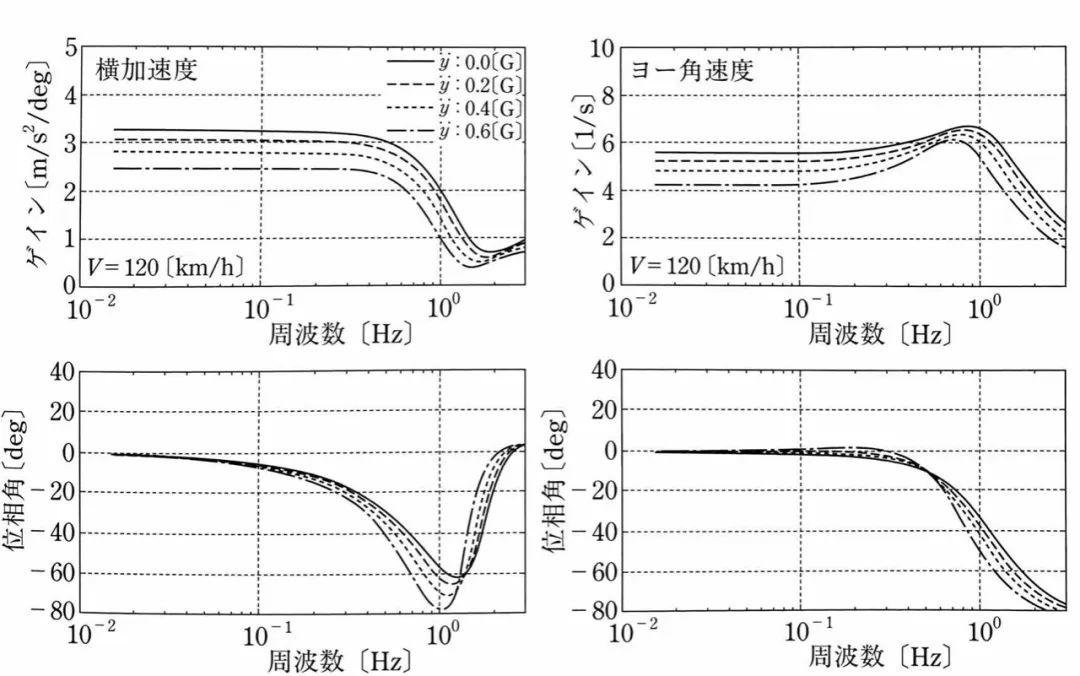
上图显示了一个车辆的横摆角速度和侧向加速度频率响应的实例。车辆作圆周运动时,不同侧向加速度值情况下车辆的动态特性,可以看出轮胎非线性特性的影响。由于轮胎对侧偏角β呈非线性的饱和特性,车辆动态特性随着侧向加速度的变化将发生明显的改变。
结
现代汽车复杂的电子系统能够浪漫和文明吗?实际上,驾驶乐趣是一种更加纯粹的体验。澎湃的动力,大风的呼啸,强劲而纯粹的汽车魅力渐行渐远。
汽车操控和设计是一项庞大的系统工程,其难度丝毫不亚于汽车电子系统,并浸透着人类的智慧。移动机器的科技只是不断变换着外衣。
只有将目光从华丽的外表移开,才能用心灵和精神去提炼简练而抽象的内涵。这就是本文我们试图探索的——理论之美。
创造美丽的事物往往没有目标,没有方向。创造其实是在不断制定美的标准。技术也是一样的——工程的训练最重要的是培养内涵,而不是数学公式。
学习对技术工作的品味和感觉。只有这样,你欣赏的东西,别人才会欣赏。
完
更多相关文章推荐
-
Part 3 | 无人车安全之战 — AI觉醒的前夜,人类还在沉睡?

本篇文章来源于微信公众号: 几何四驱




























